
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Задача №1
Задача №1
Абсолютно жесткий горизонтальный брус опирается на шарнирно неподвижную опору и прикреплен к двум стержням при помощи шарниров. Найти допускаемую нагрузку.
Дано:
А=10-3 м2 , с=1,0 м, а =2,2 м , α=45° , в =3,2 м.
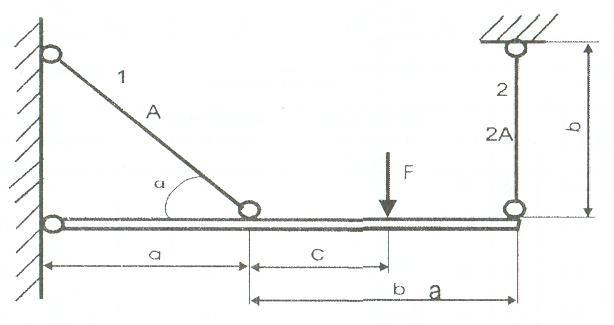
Решение: 1.
Найдем усилия и напряжения в стержнях, выразив их через F. Представим силовую схему и схему деформации системы. Из уравнения равновесия ΣМ0 =0 (1).
N2 *5,4-F*3,2 + Nl *sin450*2,2 = 0 (1)
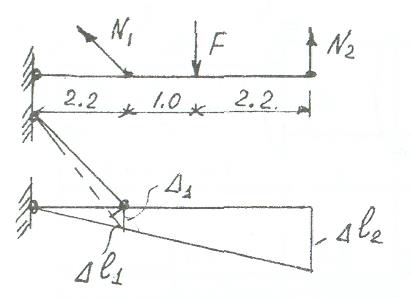
и условия совместности деформаций
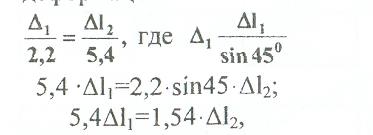
используя закон Гука 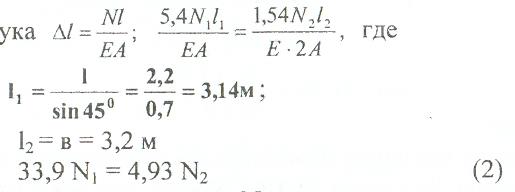
Решая совместно (1) и (2) находим N1 N2:
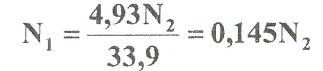
подставляем в (1)
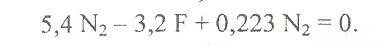
Отсюда 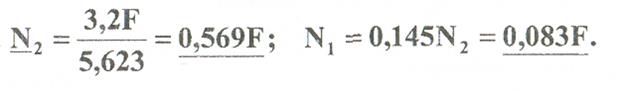
Находим напряжения в стержнях:
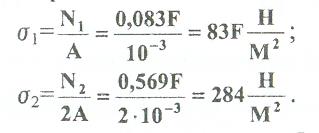
2.Найдём допускаемую нагрузку Fдоп приравняв большее из напряжений в двух стержнях допускаемому напряжению[σ]=160 Мпа(16кН/см2). σ2 =[σ] 284 Fдоп = 160-106 Fдоп =563,3KH (3)
Задача № 2
К стальному валу приложены четыре момента. Дано: а=1Лм; с=1,1м; Т2 = 2,2кНм ; Т4 = 0,2 кНм;
b = 1,1м; Т1=5,2кНм; Т3=1,2кНм; [τ] = 3 кН/см2.
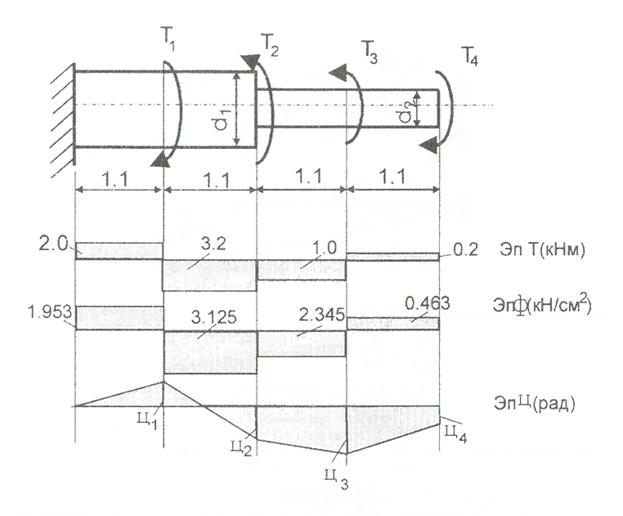 Решение: 1). Строим эпюру крутящих моментов, для чего рассматриваем вал со свободного конца. Вал имеет четыре участка, для них и составляем уравнение равновесия.
Решение: 1). Строим эпюру крутящих моментов, для чего рассматриваем вал со свободного конца. Вал имеет четыре участка, для них и составляем уравнение равновесия.
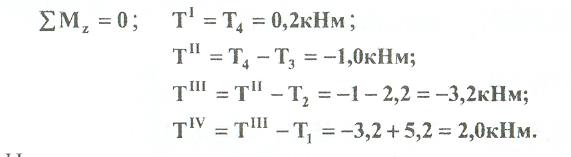 2). Исходя из условия прочности: Т„
2). Исходя из условия прочности: Т„
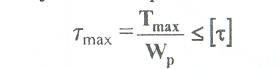 (1), где
(1), где
Tmax - максимальный крутящий момент;
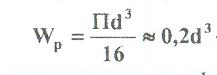 - полярный момент сопротивления.
- полярный момент сопротивления.
Находим диаметры:
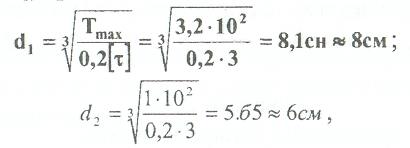
т.е. для первого и второго d2= 6см, для третьего и четвёртого d1 = 8см. 3). Строим эпюру касательных напряжений:
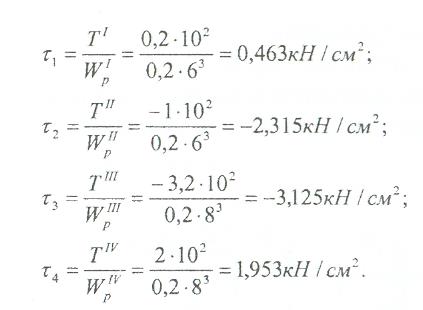
4). Строим эпюру углов закручивания приняв G = 0,4Е=8*103 кН/см2
 (2),
(2),
где Т - крутящий момент на участке,
G - модуль упругости при сдвиге,
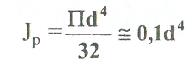 - полярный момент инерции.
- полярный момент инерции.
Угол поворота начинаем определять от заделки.
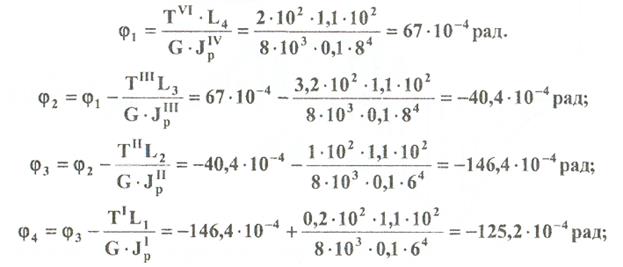 Полученные углы в масштабе наносим на эпюру ф, считая начало отсчёта в заделке.
Полученные углы в масштабе наносим на эпюру ф, считая начало отсчёта в заделке.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|