
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примечания.. ОГРАНИЧЕННОСТЬ ФУНКЦИЙ.
Примечания.
1) Если число Т является периодом функции, то каждое из чисел Тn при целом n≠0 также является периодом функции.
2) Постоянная функция (у = const) имеет периодом любое число Т≠0, но не имеет наименьшего периода.
3) Если график периодической функции построен для промежутка [а; а+Т] оси ОХ, имеющего длину Т, равную периоду функции, то весь график этой функции может быть получен повторением построенного графика в каждом из промежутков а+Тп < х < а + Т +Тп, где п — целое.
4) Если функции f(x) и g(x) имеют один и тот же период Т, то число T является периодом (возможно, не наименьшим) их суммы, разности, произведения и частного.
5) Если функция f(x) имеет период T1, а функция g(x) имеет период Т2, то для нахождения периода суммы этих функций надо найти число, которое нацело делится на T1 и Т2.
Рассмотрим на графике примеры периодических функций:

Функция у=cos(x) - периодическая функция T=2p
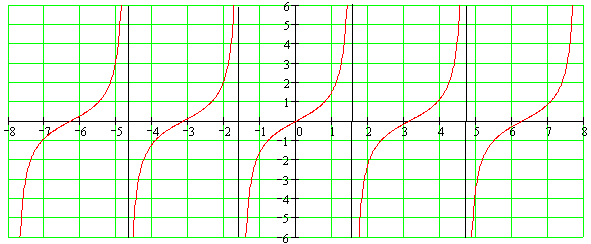
Функция у=tg(x) - периодическая функция T=p
ОГРАНИЧЕННОСТЬ ФУНКЦИЙ.
Функция y=f(x) называется ограниченной, если существуют числа М и м, такие что, для любых х из области определения функции выполняется неравенство м≤f(x)≤M
Функция y=f(x) называется ограниченной сверху, если существует число М, такое что, для любых х из области определения функции выполняется неравенство f(x)≤M
Функция y=f(x) называется ограниченной снизу, если существует число м, такое что, для любых х из области определения функции выполняется неравенство f(x)≥м
Если такие числа не существуют, то функция называется неограниченной.
Посмотрим на графиках примеры ограниченных функций:
1) Функция у=cos(x) ограниченная Е(у)=[-1;1]
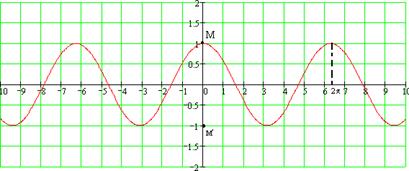
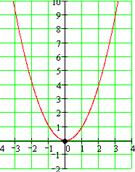
2) Функция у=х2 ограниченная снизу Е(у)=[0;+∞)
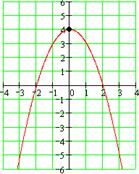
3) Функция у=4-х2 ограниченная сверху Е(у)=(-∞;4]
4) Функция у=4х+1 неограниченная Е(у)=(-∞;+∞)
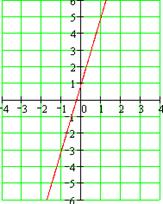
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|