
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ФУНКЦИИ
ЧЕТНОСТЬ И НЕЧЕТНОСТЬ ФУНКЦИИ
Четнойназывается функция у = f(x), если выполнены два условия:
1) область определения симметрична относительно начала координат, то есть если значение х входит в область определения, то и (-х) ей принадлежит: {х; -х}Î D(y);
2) противоположным значениям аргумента соответствуют равные значения функции, то есть
f(-х)=f(х) для любого х из области определения функции.
Графики четных функций симметричны относительно оси OY, так как, если точка (х; у) принадлежит графику функции, то по определению, ему принадлежит и точка с координатами (-х;у):
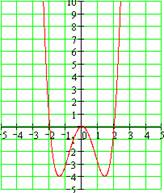
| Например, четными являются функции: а) у=х2– 4, так как f(–x)=(–x)2 –4 = x2 – 4 = f(х); б) y=5 – |х| , так как f(–x)=5 – |–x|=5 – |x|= f(х); в) у = 8; г) у = cosx. |
Нечетнойназывается функция у = f(x), если выполнены два условия:
1) область определения симметрична относительно начала координат, то есть {х; –х}Î D(y);
2) противоположным значениям аргумента соответствуют противоположные значения функции f(-x) = -f(x) для любого х из области определения.
График нечетной функции симметричен относительно начала координат. Если взять любую точку А графика нечетной функции, соединить с началом координат, затем продолжить за (0; 0) на такое же расстояние, то получим точку В, которая лежит на построенном графике нечетной функции.
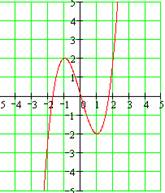
| Например, нечетными будут функции:
а) у =х3, так как f(–x)=(–x)3 = –x3 = – f(х);
б) у= 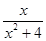 , так как f(–x)= , так как f(–x)= 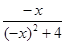 = – = – 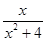 = – f(х);
в) у = х;
г) у = sinx;
д) у = 0,5 tg х. = – f(х);
в) у = х;
г) у = sinx;
д) у = 0,5 tg х.
|
Если не выполняются условия, указанные в определениях 1 или 2, то функция называется функцией общего вида, или ни четной ни нечетной
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|