Совместные и несовместные события. Противоположные события. Полная группа событий

2. Совместные и несовместные события. Противоположные события. Полная группа событий

События называют несовместными, если в одном и том же испытании появление одного из событий исключает появление других событий.

Простейшим примером несовместных событий является пара противоположных событий.

Событие, противоположное данному, обычно обозначается той же латинской буквой с чёрточкой вверху.

Например:

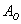– в результате броска монеты выпадет орёл;
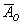– в результате броска монеты выпадет решка.

Совершено ясно, что в отдельно взятом испытании появление орла исключает появление решки (и наоборот), поэтому данные события и называются несовместными.

Противоположные события легко формулируются из соображений элементарной логики:

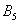– в результате броска игрального кубика выпадет 5 очков;
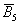– в результате броска игрального кубика выпадет число очков, отличное от пяти

Либо пять, либо не пять – третьего не дано, т.е. события несовместны и противоположны.

Множество несовместных событий образуют полную группу событий, если в результате отдельно взятого испытания обязательно появится одно из этих событий. Очевидно, что любая пара противоположных событий (в частности, примеры выше) образует полную группу. Однако в различных задачах с одним и тем же объектом могут фигурировать разные события, например, для игрального кубика характерно рассмотрение следующего набора:

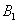– в результате броска игрального кубика выпадет 1 очко;
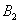– … 2 очка;
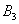– … 3 очка;
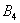– … 4 очка;
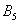– … 5 очков;
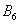– … 6 очков.

События 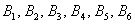несовместны (поскольку появление какой-либо грани исключает одновременное появление других) и образуют полную группу (так как в результате испытания непременно появится одно из этих шести событий).

элементарностьисхода (события). ещё одно важное понятие

Если совсем просто, то элементарное событие «нельзя разложить на другие события». Например, события 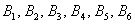элементарны, но событие 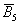не является таковым, так как подразумевает выпадение 1, 2, 3, 4 или 6 очков (включает в себя 5 элементарных исходов).

Совместные события менее значимы с точки зрения решения практических задач, но обходить их стороной не будем. События называются совместными, если в отдельно взятом испытании появление одного из них не исключает появление другого

Например:

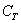– из колоды карт будет извлечена трефа;
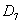– из колоды карт будет извлечена семёрка.

Если быть совсем лаконичным, одно не исключает другого.

Понятие совместности охватывает и бОльшее количество событий:

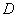– завтра в 12.00 будет дождь;
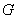– завтра в 12.00 будет гроза;
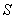– завтра в 12.00 будет солнце.

перечисленные события совместны и попарно, т.е. может быть только ливень с грозой или грибной дождик, или погромыхает неподалёку на фоне ясного неба.

Операция сложения событийозначает логическую связку ИЛИ,
а операция умножения событий – логическую связку И.

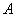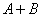1) Суммой двух событий и называется событие которое состоит в том, что наступит или событие 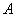или событие или оба события одновременно. В том случае, если события несовместны, последний вариант отпадает, то есть может наступить или событие 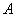или событие .

Правило распространяется и на бОльшее количество слагаемых, например, событие 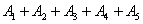состоит в том, что произойдёт хотя бы одно из событий , а если события несовместны – то одно и только одно событие из этой суммы: или событие 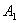, или событие 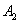, или событие 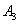, или событие 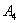,или событие .

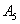--Событие 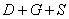состоит в том, что завтра в 12.00 наступит ХОТЯ БЫ ОДНО из суммируемых совместных событий, а именно:

– или будет только дождь / только гроза / только солнце;
– или наступит только какая-нибудь пара событий (дождь + гроза / дождь + солнце / гроза + солнце);
– или все три события появятся одновременно.

То есть, событие 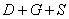включает в себя 7 возможных исходов.

2) Произведением двух событий 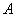и называют событие 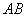, которое состоит в совместном появлении этих событий, иными словами, умножение 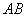означает, что при некоторых обстоятельствах наступит и событие 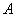, и событие . Аналогичное утверждение справедливо и для бОльшего количества событий, так, например, произведение 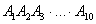подразумевает, что при определённых условиях произойдёт и событие 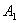, и событие 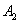, и событие 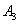, …, и событие .

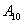Рассмотрим испытание, в котором подбрасываются две монеты и следующие события:

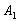– на 1-й монете выпадет орёл;
– на 1-й монете выпадет решка;
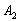– на 2-й монете выпадет орёл;
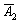– на 2-й монете выпадет решка.

Тогда:
– событие 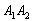состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет орёл;
– событие 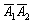состоит в том, что на обеих монетах (на 1-й и на 2-й) выпадет решка;
– событие состоит в том, что на 1-й монете выпадет орёл и на 2-й монете решка;
– событие 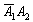состоит в том, что на 1-й монете выпадет решка и на 2-й монете орёл.

Нетрудно заметить, что события несовместны (т.к. не может, например, выпасть 2 орла и в то же самое время 2 решки) и образуют полную группу (поскольку учтены все возможные исходы броска двух монет). Давайте просуммируем данные события: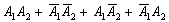

Таким образом, сумму 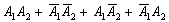легко прочитать понятным человеческим языком: «выпадут два орла или две решки или на 1-й монете выпадет орёл и на 2-й решка или на 1-й монете выпадет решка и на 2-й монете орёл » пример, когда в одном испытании задействовано несколько объектов, в данном случае – две монеты.

Другая распространенная в практических задачах схема – это повторные испытания, когда, например, один и тот же игральный кубик бросается 3 раза подряд.

например, один и тот же игральный кубик бросается 3 раза подряд. В качестве демонстрации рассмотрим следующие события:

– в 1-м броске выпадет 4 очка;
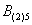– во 2-м броске выпадет 5 очков;
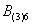– в 3-м броске выпадет 6 очков.

Тогда событие состоит в том, что в 1-м броске выпадет 4 очка и во 2-м броске выпадет 5 очков и в 3-м броске выпадет 6 очков. Очевидно, что в случае с кубиком будет значительно больше комбинаций (исходов), чем, если бы мы подбрасывали монету. (В зависимости от правил составления можно выделить три типа комбинаций: перестановки, размещения, сочетания.)

⇐ Предыдущая 123 Следующая ⇒