Метод Рунге – Кутта

Метод Рунге – Кутта

Основная идея этого метода такова: вместо использования в рабочих формулах частных производных функции f(х, у) использовать лишь саму эту функцию, но на каждом шаге вычислять ее значения в нескольких точках.

Проиллюстрируем это на примере одного из возможных методов второго порядка. Для метода Эйлера путем простейшей правосторонней аппроксимации производной имеем: .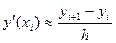

В это выражение входят значения функции в двух точках. Если взять в правой части уравнения (1) значение f(х, у) в точке с номером i, то придем к методу Эйлера. Однако можно рассудить и иначе: раз для аппроксимации производной взяты две точки, то лучшей аппроксимацией правой части уравнения будет полусумма 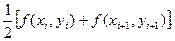. Тогда для нахождения у_i₊₁ получим равенство 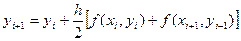. Поскольку оно представляет собой уравнение для у_i₊₁, то решать его можно методом итераций, причем в качестве первого приближения взять то значение y_i_+l, которое определяется методом Эйлера. В итоге получим расчетные формулы нового метода, обеспечивающего пошаговое интегрирование дифференциального уравнения (1).

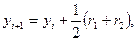(5)

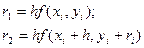где (6)

Формула (5) - лишь одна из множества возможных формул Рунге - Кутта 2-го порядка. Разные формулы Рунге - Кутта одного и того же порядка будут давать при использовании различные числовые значения, но все они одного порядка точности. Чем выше порядок формул Рунге - Кутта, тем более точные значения они дают. На практике соблюдается некоторый компромисс между высоким порядком формул и их громоздкостью, с одной стороны, и объемом вычислений по ним для достижения заданной точности, с другой. Ниже приведена одна из самых популярных формул 4-го порядка, часто называемая просто, без уточнений, формулой Рунге - Кутта:

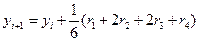(7)

где

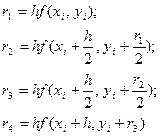(8)

причем вначале последовательно вычисляются r₁, r₂, r₃, r₄, а лишь затем y_i₊₁ - по формуле (7).

Общий недостаток методов Рунге-Кутта — отсутствие простых способов оценки погрешности метода. Погрешность на одном шаге оценить сравнительно нетрудно, гораздо труднее оценить накопление погрешностей на протяжении многих шагов. Широко используемый на практике для этих методов полуэмпирический способ контроля точности — двойной счет. Допустим, что 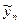— точное решение уравнения при х = х₀ + nh. Тогда для рассмотренного выше метода 4-го порядка 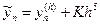, где верхний индекс означает шаг, с которым вычислено приближенное значение. Точно так же при решении с шагом :

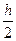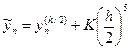Отсюда получаем: .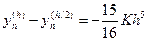

Следовательно, ошибка при вычислении с шагом 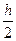есть

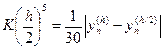(9)

Из формулы (9), в частности, следует, что при достаточно малом h и малых погрешностях вычислений решение уравнения (1), полученное методом Рунге-Кутта 4-го порядка по формулам (7) – (8), будет близким к точному.

⇐ Предыдущая 1 23