Тема 2.5 Численное решение обыкновенных

Тема 2.5 Численное решение обыкновенных

дифференциальных уравнений

Постановка задачи

Пусть дано дифференциальное уравнение первого порядка:

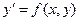. (1)

Основная задача, связанная с этим уравнением, известна как задача Коши: найти решение уравнения (1) в виде функции у(х),удовлетворяющей начальному условию

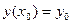(2)

Геометрически это означает, что требуется найти интегральную кривую у = у(х), проходящую через заданную точку M₀ (x₀, у₀), при выполнении равенства (1). Существование и единственность решения задачи Коши для уравнения (1) обеспечиваются следующей теоремой.

Теорема Пикара. Если функция f(x, у) определена и непрерывна в некоторой плоской области G, определяемой неравенствами ׀х-х₀׀ ≤ а, ׀y-y₀׀ ≤ b, и удовлетворяет в этой области условию Липшица по у: существует такое положительное число М, что для любых точек (х; у₁) G и (х; у₂) G: |f(x,y₁) - f(x,y₂)| ≤ M·|y₁-y₂|, то на некотором отрезке |х - х₀| ≤ h существует, и притом только одно, решение у = у(х) уравнения (1), удовлетворяющее начальному условию у₀= у(x₀).

Число М называется константой Липшица.

Если f(х, у) имеет ограниченную в G производную по у, то 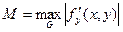. Величина h вычисляется по формул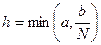е , где .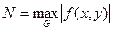

Существует несколько классов дифференциальных уравнений первого порядка, для которых решение может быть найдено аналитически (уравнения с разделяющимися переменными, однородные, линейные, в полных дифференциалах). Даже для таких уравнений решение не всегда удается довести до вида у = у(х), где у(x) — функция, с которой удобно работать дальше. Многие же дифференциальные уравнения, к которым приводят математические модели реальных процессов, не относятся к указанным классам и аналитически решены быть не могут. Тем более это утверждение справедливо для систем дифференциальных уравнений и для уравнений старших порядков. По этой причине разработаны многочисленные методы приближенного решения дифференциальных уравнений. В зависимости от формы представления решения, эти методы подразделяются на три основные группы:

- аналитические методы, применение которых дает приближенное решение дифференциального уравнения в виде формулы;

- графические методы, дающие приближенное решение в виде графика;

- численные методы, когда искомая функция получается в виде таблицы.

12 3 Следующая ⇒