Метод Эйлера

Метод Эйлера

В основе метода ломаных Эйлера лежит идея графического построения решения дифференциального уравнения, однако этот метод дает одновременно и способ нахождения искомой функции в численной (табличной) форме.

Пусть дано уравнение (1) с начальным условием (2) (т.е. поставлена задача Коши). Вначале найдем простейшим способом приближенное значение решения в некоторой точке х₁ = x₀ + h, где h достаточно малый шаг. Уравнение (1) совместно с начальным условием (2) задают направление касательной к искомой интегральной кривой в точке М₀(х₀,y₀). Двигаясь вдоль этой касательной, получим приближенное значение решения в точке х_1:

y₁= y₀+ hf (x₀, y₀). (3)

Располагая приближенным решением в точке М₁(х_1,у₁), можно повторить описанную выше процедуру: построить прямую, проходящую через эту точку под углом, определяемым условием tgβ = f(x₁, y₁), и по ней найти приближенное значение решения в точке х₂= x₁+ h. Эта прямая не есть касательная к реальной интегральной кривой, поскольку точка М₁ нам недоступна. Однако если h достаточно мало, то получаемые приближения будут близки к точным значениям решения.

Продолжая этот процесс, построим систему равноотстоящих точек x_i= х₀+ ih, где (i = 0,1,2,..., n). Получение таблицы значений искомой функции у(х) по методу Эйлера заключается в циклическом применении пары формул:

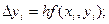(4)

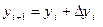Геометрическая иллюстрация метода Эйлера приведена на рисунке. Вместо интегральной кривой в реальности получается совокупность прямых (так называемая ломаная Эйлера).

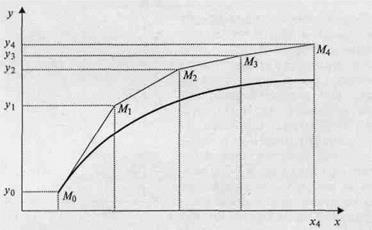
Методы численного интегрирования дифференциальных уравнений, в которых решение получается от одного узла к другому, называются пошаговыми. Метод Эйлера — простейший представитель семейства пошаговых методов.

Оценка погрешности метода при таком элементарном рассмотрении невозможна даже на первом шаге. Кроме того, особенностью любого пошагового метода является то, что, начиная со второго шага, исходное значение у_i в формуле (4) само является приближенным, т.е. погрешность на каждом следующем шаге систематически возрастает.

Наиболее используемым эмпирическим методом оценки точности как метода Эйлера, так и других пошаговых методов приближенного численного интегрирования обыкновенных дифференциальных уравнений является способ двойного прохождения заданного отрезка — с шагом h и с шагом h/2. Совпадение соответствующих десятичных знаков в полученных двумя способами результатах дает эмпирические основание считать их верными (хотя полной уверенности в этом быть не может).

⇐ Предыдущая 123 Следующая ⇒