
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Доказательство.. Замечание.. Правило Лопиталя
Доказательство.
1) Покажем сначала, что 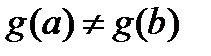 , т.е. что формула имеет смысл. Покажем от противного.
, т.е. что формула имеет смысл. Покажем от противного.
Пусть 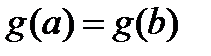 , тогда функция
, тогда функция 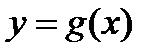 удовлетворяет всем трем условиям теоремы Ролля, т.е. существует точка
удовлетворяет всем трем условиям теоремы Ролля, т.е. существует точка 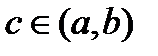 , в которой
, в которой 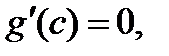 а это противоречит условию, что
а это противоречит условию, что 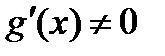 на
на 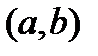 . Отсюда,
. Отсюда, 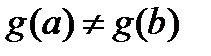 .
.
2) Рассмотрим на 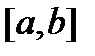 следующую вспомогательную функцию:
следующую вспомогательную функцию: 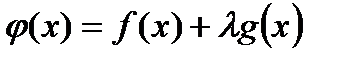 , где
, где 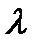 выберем так, чтобы выполнялось равенство:
выберем так, чтобы выполнялось равенство: 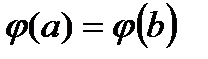 , равносильное следующему:
, равносильное следующему: 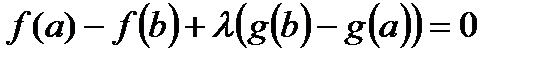 . Отсюда:
. Отсюда:
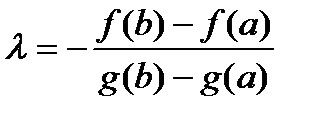 . (**)
. (**)
Т.к. функция 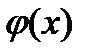 непрерывна на отрезке
непрерывна на отрезке 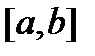 , дифференцируема на интервале
, дифференцируема на интервале 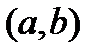 , а при значениях
, а при значениях 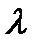 , определяемых формулой (**) принимает равные значения в концах интервала
, определяемых формулой (**) принимает равные значения в концах интервала 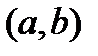 , то по теореме Ролля существует точка
, то по теореме Ролля существует точка 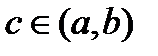 такая, что
такая, что  т.е.
т.е. 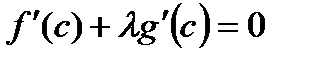 , отсюда:
, отсюда:
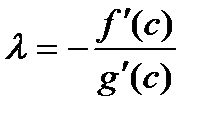 . (***)
. (***)
Сравнивая формулы (**) и (***), получим
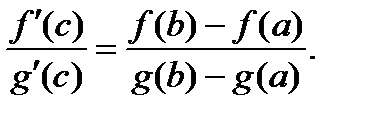
(что и требовалось доказать)
Замечание.
Формула  называется обобщенной формулой конечных приращений.
называется обобщенной формулой конечных приращений.
2. Правило Лопиталя
1. Неопределенность вида 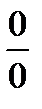 .
.
Теорема 2.1.Пусть функции 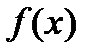 и
и 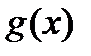 непрерывны и дифференцируемы в окрестности точки а и обращаются в нуль в этой точке:
непрерывны и дифференцируемы в окрестности точки а и обращаются в нуль в этой точке: 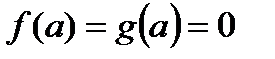 . Пусть
. Пусть 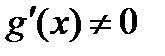 в окрестности точки а. Если существует предел
в окрестности точки а. Если существует предел 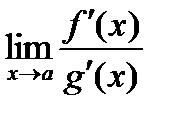 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 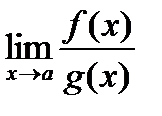 , причем справедлива формула
, причем справедлива формула
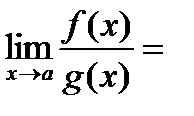
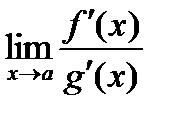 .
.
Замечание 1.Теорема справедлива при 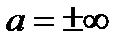 .
.
Замечание 2.Если 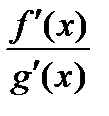 представляет собой неопределенность
представляет собой неопределенность 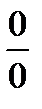 и функции
и функции 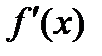 и
и 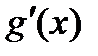 удовлетворяют условиям теоремы 2.1, то
удовлетворяют условиям теоремы 2.1, то
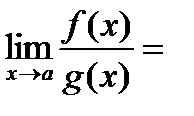
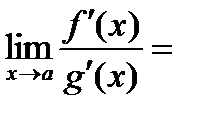
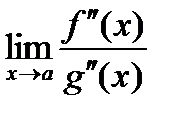 .
.
2. Неопределенность вида 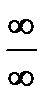 .
.
Теорема 2.2. Пусть функции 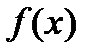 и
и 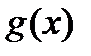 непрерывны и дифференцируемы в окрестности точки а (кроме, может быть, самой точки а), в этой окрестности
непрерывны и дифференцируемы в окрестности точки а (кроме, может быть, самой точки а), в этой окрестности 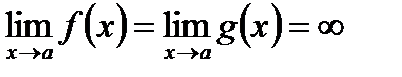 . Пусть
. Пусть 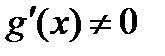 в окрестности точки а. Если существует предел
в окрестности точки а. Если существует предел 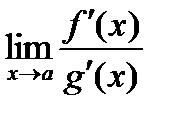 (конечный или бесконечный), то существует и предел
(конечный или бесконечный), то существует и предел 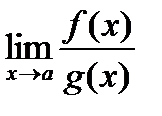 , причем справедлива формула
, причем справедлива формула
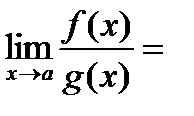
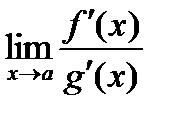 .
.
Замечание 3.Неопределенности вида 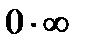 ,
, 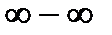 ,
, 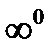 ,
, 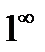 ,
, 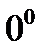 часто удается свести к неопределенностям вида
часто удается свести к неопределенностям вида 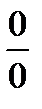 и
и 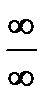 с помощью тождественных преобразований.
с помощью тождественных преобразований.
Примеры.
1. 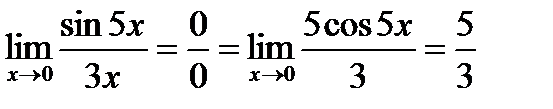 .
.
2. 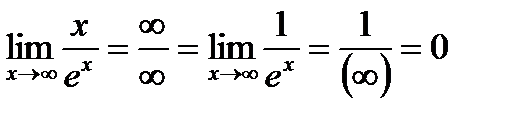 .
.
3. 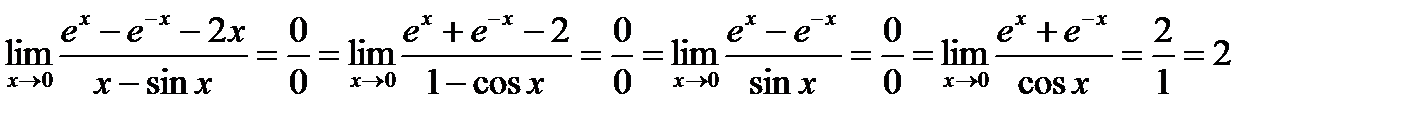 .
.
4. 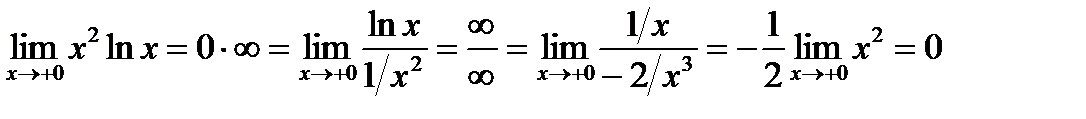 .
.
5.  . Пусть
. Пусть 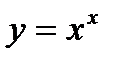 , прологарифмируем обе части равенства:
, прологарифмируем обе части равенства:  . Найдем предел
. Найдем предел 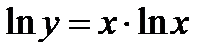 :
:
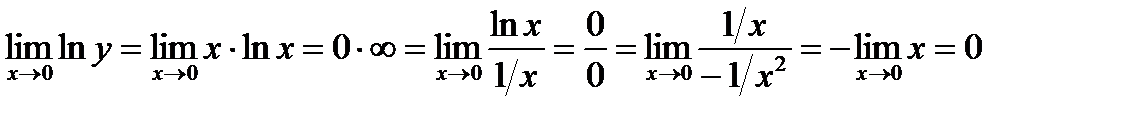 .
.
Следовательно, 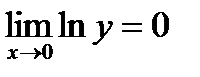 , отсюда
, отсюда 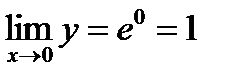 , т.е.
, т.е. 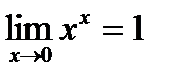 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|