
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Основные теоремы о дифференцируемых функциях
1. Основные теоремы о дифференцируемых функциях
1.1. Теорема Ролля (Ролль Мишель, француз, 1652 – 1719 г.)
Если функция 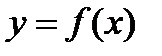 непрерывна на отрезке
непрерывна на отрезке 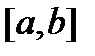 , принимает на концах этого отрезка равные значения, т.е.
, принимает на концах этого отрезка равные значения, т.е.
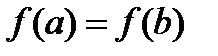 , (1)
, (1)
дифференцируема на интервале 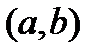 , тогда существует точка
, тогда существует точка 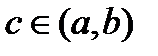 такая, что
такая, что
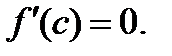
Доказательство.
Пусть 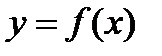 непрерывна на отрезке
непрерывна на отрезке 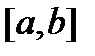 , тогда по второй теореме Вейерштрасса она достигает на этом отрезке своего максимального и минимального значений, т.е. существуют точки
, тогда по второй теореме Вейерштрасса она достигает на этом отрезке своего максимального и минимального значений, т.е. существуют точки 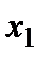 и
и 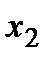 , принадлежащие отрезку
, принадлежащие отрезку 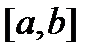 такие, что
такие, что 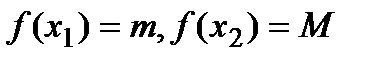 , причем
, причем 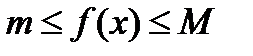 .
.
Рассмотрим два случая:
1) 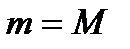 , следовательно,
, следовательно, 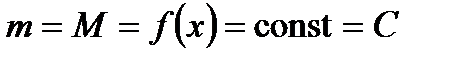 , тогда
, тогда 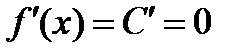 в любой точке
в любой точке 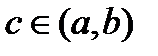 .
.
2) 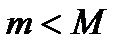 , при этом
, при этом 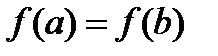 , поэтому
, поэтому 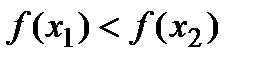 . В силу условия (1) хотя бы одна точка
. В силу условия (1) хотя бы одна точка 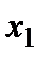 или
или 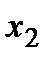 является внутренней точкой
является внутренней точкой 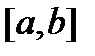 . Пусть, например, точка
. Пусть, например, точка 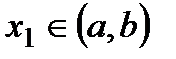 . Тогда существует такая δ-окрестность точки
. Тогда существует такая δ-окрестность точки 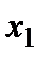 , в которой выполняется условие
, в которой выполняется условие 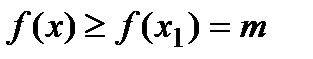 для
для 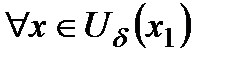 . Тогда:
. Тогда:
если 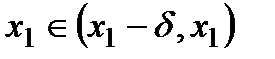 , то
, то 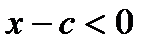 и
и 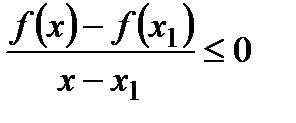 ;
;
если 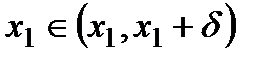 , то
, то 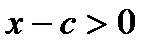 и
и 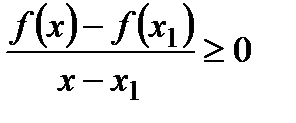 .
.
Т.к. функция 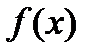 дифференцируема в точке
дифференцируема в точке 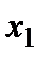 , то в этой точке существует предел, при этом существуют односторонние пределы:
, то в этой точке существует предел, при этом существуют односторонние пределы:
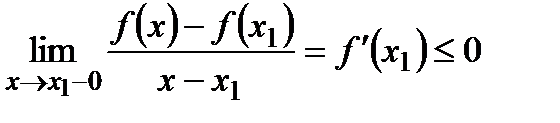 ,
,
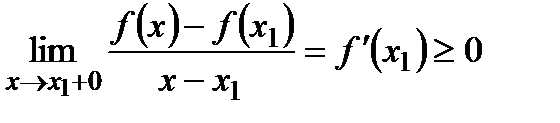 .
.
Оба предела равны между собой только в случае, когда 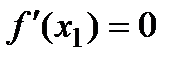 , т.е. условие (1) выполняется при
, т.е. условие (1) выполняется при 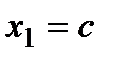 .
.
Аналогично рассматривается случай, когда 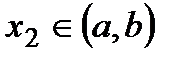 .
.
(что и требовалось доказать)
| х |
| y |
| M |
| y=f(х) |
| с |
| O |
1.Геометрический смысл теоремы: у графика функции, удовлетворяющей всем трем условиям теоремы Ролля, существует точка 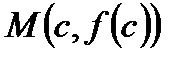 , в которой касательная параллельна оси Ох.
, в которой касательная параллельна оси Ох.
2. Все три условия теоремы существенны. Например, рассмотрим функцию 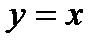 на отрезке
на отрезке 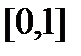 . Данная функция непрерывна на отрезке
. Данная функция непрерывна на отрезке 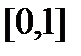 , дифференцируема на интервале
, дифференцируема на интервале 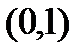 , но
, но 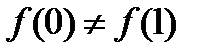 , поэтому не существует точки
, поэтому не существует точки 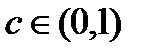 , в которой
, в которой 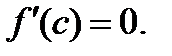
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|