
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Теорема Лагранжа (Жозеф Луи Лагранж, француз, 1736 – 1813 г.р.)
1.2. Теорема Лагранжа (Жозеф Луи Лагранж, француз, 1736 – 1813 г.р.)
Если функция 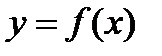 непрерывна на отрезке
непрерывна на отрезке 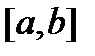 , дифференцируема на интервале
, дифференцируема на интервале 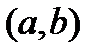 , то в этом интервале найдется хотя бы одна точка
, то в этом интервале найдется хотя бы одна точка 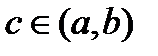 такая, что
такая, что
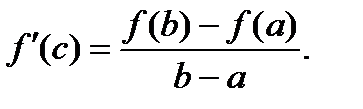
Доказательство.
Для доказательства введем в рассмотрение на 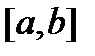 следующую вспомогательную функцию:
следующую вспомогательную функцию:
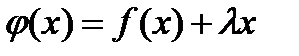 ,
,
где 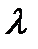 выберем таким, чтобы выполнялось условие
выберем таким, чтобы выполнялось условие 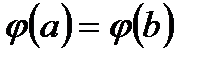 , т.е.
, т.е. 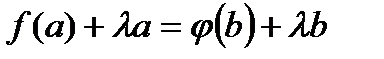 .
.
Отсюда находим:
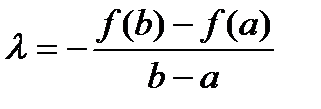 . (*)
. (*)
Т.к. 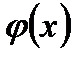 непрерывна на отрезке
непрерывна на отрезке 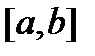 , дифференцируема на интервале
, дифференцируема на интервале 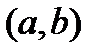 и принимает в концах этого интервала равные значения, то по теореме Ролля существует точка
и принимает в концах этого интервала равные значения, то по теореме Ролля существует точка 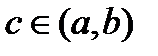 такая, что выполняется равенство:
такая, что выполняется равенство:
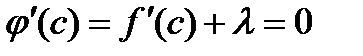 .
.
Отсюда, в силу условия (*) получим:
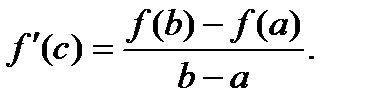
(что и требовалось доказать)
| f(b)-f(a) |
| b - a |
| f(b) |
| f(a) |
| f(c) |
| a |
| b |
| c |
| O |
| y = f(x) |
| M1 |
| M2 |
| M |
| l |
| α |
| α |
1.Величина 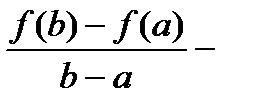 угловой коэффициент секущей
угловой коэффициент секущей 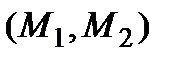 , проходящей через точки
, проходящей через точки 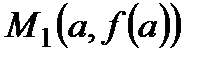 и
и 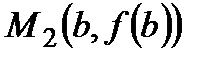 к кривой
к кривой 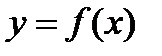 ,
, 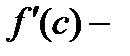 угловой коэффициент касательной l к графику функции
угловой коэффициент касательной l к графику функции 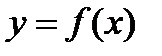 в точке
в точке 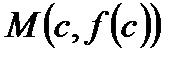 , а так как
, а так как 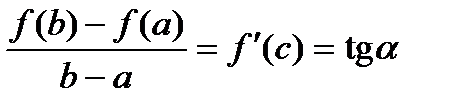 , то обязательно существует точка
, то обязательно существует точка 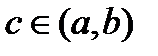 такая, что касательная l к кривой в точке
такая, что касательная l к кривой в точке 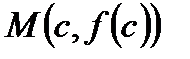 параллельна секущей
параллельна секущей 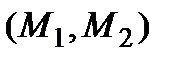 .
.
Таких точек с может быть несколько, но, по крайней мере, одна существует.
2. Равенство 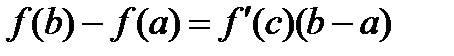 называется формулой конечных приращений Лагранжа.
называется формулой конечных приращений Лагранжа.
1. 3. Теорема Коши (Огюстен Луи Коши, француз, 1789 – 1857 г.р.)
Если функции 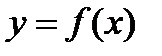 ,
, 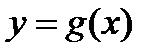 непрерывны на отрезке
непрерывны на отрезке 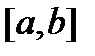 , дифференцируемы на интервале
, дифференцируемы на интервале 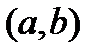 , причем
, причем 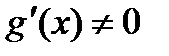 во всех точках этого интервала, тогда найдется хотя бы одна точка
во всех точках этого интервала, тогда найдется хотя бы одна точка 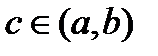 такая, что справедлива формула:
такая, что справедлива формула:
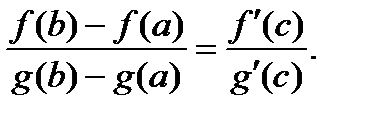
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|