
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Тема 8. Визначення еквівалентності відсоткових ставок
Тема 8. Визначення еквівалентності відсоткових ставок
Система еквівалентних ставок складається з таких елементів еквівалентності:
· простих ставок;
· простих і складних ставок;
· складних ставок;
· дискретних і неперервних ставок
Треба пам’ятати, що виведення формул еквівалентності ставок у всіх випадках базується на рівності взятих попарно відповідних множників наростання.
Формула простої ставки відсотків, що еквівалентна простій обліковій ставці, матиме такий вигляд:
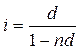 .
.
Формула простої облікової ставки, що еквівалентна простій ставці відсотків, має такий вигляд 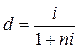 .
.
Розглянемо формули еквівалентності для простих і складних ставок відсотків.
Зв’язок між еквівалентними ставками відсотків визначається за такими формулами:
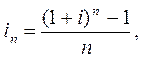
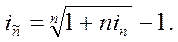
Якщо еквівалентна простій ставці складна ставка нараховується m разів на рік, тоді:
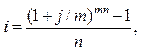
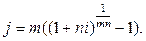
Формули еквівалентності простої облікової ставки і ставки складних відсотків мають такий вигляд:
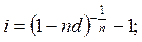
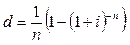
Якщо складні відсотки нараховуються m разів на рік, тоді при рівних часових базах нарахування відсотків формули еквівалентності будуть такими:
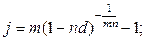
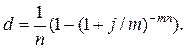
Еквівалентність складних відсоткових і складної облікової ставки:
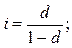
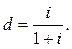
Якщо відсоткові ставки змінюються з часом, то еквівалентна їм ставка являє собою середню ставку (і), яка дає за певний період такий самий дохід. Дану середню знайдемо на основі рівності відповідних множників наростання. Нехай за періоди n1, n2, ..., nk нараховуються прості відсотки за ставками i1, i2, ..., ik:
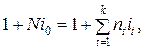 де
де 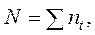
отримаємо еквівалентну ставку
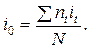
Аналогічно для простих облікових ставок d1, d2, .., dk знаходимо їх середню d0:
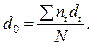
Консолідуванням називається об’єднання кількох боргових зобов’язань в одне, а розмір об’єднаного платежу називається консолідованим платежем.
Нехай платежі S1, S2, ...., Sn зі строками відповідно n1, n2, ..., nm об’єднуються в один у сумі S0 i строком n0.
Сума консолідованих платежів за умови, що n0 > n1, n2, ...., nm, для простої ставки відсотків становить 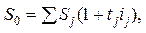
де tj — часовий інтервал між строками n0 i nj, tj = n0 – nj.
Для простої облікової ставки:
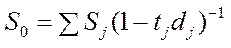 ;
;
для складної ставки відсотків:
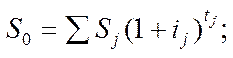
для складної облікової ставки:
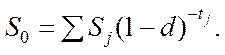
У загальному випадку величину S0 знаходимо як суму нарощених або дисконтованих платежів Sj:
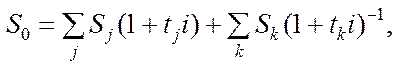
де Sj — сума об’єднаних платежів зі строками nj, nj < n0; Sk — сума платежів, які об’єднуються зі строками nk, nk > n0. Відповідно tj = n0 – nj; tk = nk – n0.
Завдання 126-134.
126. Строк сплати за векселем 150 днів. Операція обліку принесла 30 % доходу. Визначити облікову ставку векселя.
127. Вексель ураховано за ставкою 10 % річних (часова база 360 днів). Строк сплати за векселем — через 200 днів. Визначити ефективність даної угоди.
128. Строк сплати за векселем 150 днів. Вексель урахований за ставкою 30 %. Визначити дохідність даної операції.
129. Визначити рівень простої відсоткової ставки зі строком 5 років, якщо кредит одержано під 20 % річних.
130. Кредит одержано під 10 % річних (складна ставка відсотків). Визначити рівень простої відсоткової ставки при строках: а) 5 років; б) 5 місяців.
131. Фінансові відносини сторін не змінюються і в договорі проставлена проста ставка відсотків 10 %. Визначити річну ставку складних відсотків. Строк договору 2 роки.
132. Строк погашення векселя настає через 100 днів. Вексель ураховується за ставкою 10 % річних (часова база 360 днів). Визначити ефективність даної угоди. Як показник ефективності взяти річну складну ставку відсотків.
133. За угодою була видана позичка в розмірі 1000 грн. Угода укладена на 4 роки. За перші 2 роки передбачалось нараховувати відсотки за ставкою 10 % річних (складні відсотки). У наступні 2 роки ставка відсотків зростала щорічно на 5 п. п. За угодою сторін було вирішено замінити всі відсоткові ставки однією, при цьому не змінивши фінансових відносин сторін. Визначити суму боргу в кінці дії контракту.
134. Дві сторони вирішили спростити фінансові відносини і домовилися консолідувати чотири зобов’язання в одне. Перше зобов’язання мало вигляд угоди про видачу позички в розмірі 1000 грн на 90 днів. Угода укладена 1 квітня за ставкою простих відсотків 10 % річних. Друге зобов’язання – 1000 грн. Це угода про кредит, яку укладено 1 січня на 2 роки за ставкою складних відсотків 12 % річних. Третє зобов’язання – вексель на 500 грн, наданий 1 травня строком на 2 місяці. Облікова ставка векселя – 10 % річних. Четверте зобов’язання – вексель на 50 грн, наданий 1 квітня строком до 15 травня за обліковою ставкою 10 % річних. Консолідування всіх зобов’язань проводиться 1 червня. Визначити суму нового зобов’язання, яке необхідно погасити 1 червня.
Тема 9. Аналіз фінансових потоків
Фінансовий потік платежів, усі члени якого — позитивні величини, а часові інтервали між двома послідовними платежами постійні, називаються фінансовою рентою, або ануїтетом, незалежно від походження цих платежів, їх призначення і мети.
Сучасна величина ренти — це сума всіх членів ренти, дисконтованих на деякий момент часу, який збігається з початком ренти або попереджує його.
Формула нарощеної суми річної, звичайної, постійної ренти:
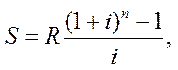
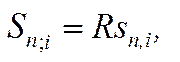
де 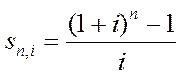 — коефіцієнт нарощення ренти.
— коефіцієнт нарощення ренти.
Коли відсотки нараховуються m разів на рік на платежі, які вносяться один раз на рік, а відсотки нараховуються за ставкою j/m. Отже, платежі з нарахованими відсотками буде в m разів більше, і:
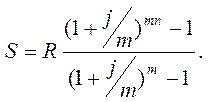
Рента р-термінова (m = 1). Визначимо нарощену суму за умови, що рента виплачується р разів на рік рівними платежами, а відсоток нараховується один раз у кінці року. Якщо річна сума платежу R, то кожний раз виплачується R/p. Формула для знаходження нарощеної суми р-термінової ренти буде такою:
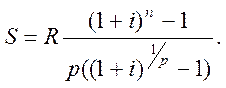
Рента р-термінова (p = m). Число членів ренти на рік дорівнює кількості нарахувань відсотків протягом року p = m.
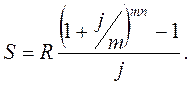
Рента р-термінова  . Загальний випадок р-термінової ренти з нарахуванням відсотків m разів на рік:
. Загальний випадок р-термінової ренти з нарахуванням відсотків m разів на рік:
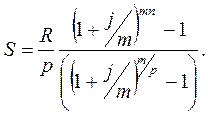
Для одних і тих самих річних виплат, тривалості ренти і ставок відсотків справедливі нерівності:
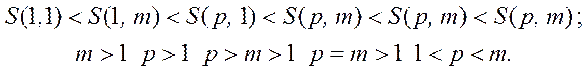
першим членом R(1 + i)–1 і знаменни-
ком (1 + i)–1 з числом членів n. Сучасна величина річної ренти визначається як сума геометричної прогресії за такою формулою:
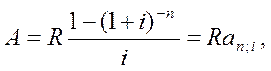
Річна рента з нарахуванням відсотків m разів на рік:
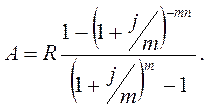
Сучасна величина р-термінової ренти (m = 1).
Якщо платежі здійснюються не один, а р разів на рік, а відсотки нараховуються один раз на рік, то коефіцієнт приведення матиме вигляд:
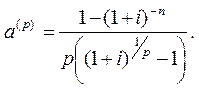
а сучасна величина ренти розраховуватиметься за формулою:
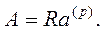
Загальний випадок знаходження сучасної величини ренти, коли відсотки нараховуються m разів, виплати відбуваються р-разів на рік, а 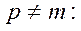
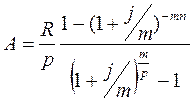 .
.
Визначення строку ренти..
Якщо рента річна і відсотки капіталізуються за річною ставкою і, то
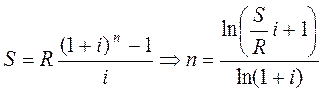 ;
;
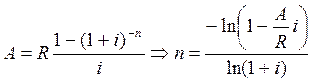 .
.
Конверсія фінансових рент. Конверсією фінансових рент називається заміна потоку рентних платежів іншим платежем. Також кілька рент можуть бути об’єднані в одну, вона повинна відповідати принципу фінансової еквівалентності.
Серед різновидів конверсій можна виокремити такі: викупівля ренти, відстрочування платежів, консолідація боргів.
Викупівля ренти— це виплата сучасної величини цієї ренти на даний момент.
Відстрочування платежів — це заміна одноразового платежу фінансовою рентою, тобто надання кредиту.. Для збереження принципу фінансової еквівалентності сучасну величину ренти прирівнюють до величини платежу, який замінюється (вартість відвантаженої продукції). Консолідація рент — це об’єднання кількох рент в одну. Принцип фінансової еквівалентності у такому разі передбачає виконання даної рівності:
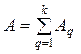 ,
,
де А — сучасна величина рент, які замінюються;
Aq — сучасна величина q-ї ренти (q = 1, 2, .., k).
При об’єднанні рент можуть виникнути найрізноманітніші задачі, зокрема: а) визначення розміру члена об’єднаної ренти; б) визначення терміну об’єднаної ренти. В обох випадках повинні бути задані інші параметри рент.
Аналіз змінних потоків платежів.Змінна рента — це рента, члени якої змінюються відповідно до якогось закону розвитку. У такому разі узагальнюючі характеристики отримають лише шляхом прямого розрахунку.
Нарощена сума:
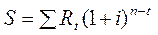 .
.
Сучасна величина:
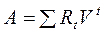 ,
,
де t — час від початку потоку платежів до моменту виплати;
Rt — сума платежу (член ренти).
Завдання 135-145
135. У кінці кожного кварталу на рахунок до банку перераховується сума грошей. Річна сума внесків 100 грн, і на ці кошти нараховуються 8 % річних. Знайти нарощену суму ренти через 10 років за умови, що відсотки на кошти на рахунку нараховуються щоквартально.
136. Необхідно визначити суму, яка потрібна для того, щоб можна було виплачувати кредитору кожні півроку 50 грн протягом 2 років, якщо на ваш рахунок у банку відсотки нараховуються щомісячно за річною ставкою 12 %.
137. Необхідно знайти нарощену суму ренти за умови, що відсотки нараховуються кожні півроку. Строк ренти — 10 років. Виплата платежів один раз на кінець року по 100 грн. Ставка, за якою нараховуються відсотки на платежі, дорівнює 10 %.
138. Строк ренти 2 роки. Річна сума ренти становить 100 грн. Нарахування відсотків щомісячне, за ставкою 12 % річних. Знайти сучасну величину ренти.
139. Рента виплачується два рази на рік. Річна сума ренти — 100 грн. Рента виплачуватиметься протягом двох років. Нарахування відсотків щомісячне, за ставкою 12 %. Визначити нарощену суму ренти.
140. Визначити величину рівних внесків, якщо необхідно до кінця десятирічного періоду створити фонд, який дорівнюватиме 100 000 грн. Ставка відсотків — 10 %.
141. Строк ренти 10 років. Виплата платежів — один раз наприкінці року по 100 грн. Ставка, за якою нараховуються відсотки по платежах, — 10 %. Визначити накопичену суму ренти.
142. Строк ренти 5 років. Нарахування відсотків у кінці року — за ставкою 5 %. Член ренти дорівнює 100 грн. Знайти сучасну величину ренти.
143. Визначити величину щомісячних внесків на спеціальний рахунок у банку для погашення поточної заборгованості в розмірі 100 000 грн. Її необхідно погасити протягом двох років. Ставка відсотків — 12 %. Відсотки нараховуються щомісячно.
144. Строк ренти 10 років. Виплата платежів — один раз наприкінці року по 100 грн. Ставка, за якою нараховуються відсотки по платежах — 10 %. Визначити накопичену суму ренти.
145. Строк ренти 5 років. Нарахування відсотків у кінці року за ставкою 5 %. Член ренти дорівнює 100 грн. Знайти сучасну величину ренти.
Тема 10. Статистична оцінка довгострокової заборгованості
Нехай накопичення коштів здійснюється шляхом регулярних щорічних внесків, на які нараховуються складні відсотки за ставкою і. Одночасно відбувається виплата відсотків, які нараховуються на борг за ставкою q. У такому разі термінова виплата складатиме:
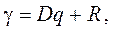 або
або 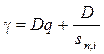 ,
,
де γ — термінова виплата; D — сума боргу, яку необхідно погасити через n років; n — строк позички (число років); q — ставка відсотків, згідно з якою кредиторові виплачується регулярний дохід з позички; R — виплата, що періодично вноситься до банку чи іншого фінансового підприємства для створення фонду погашення.
При створенні фонду погашення фігурують дві ставки відсотків: і i q. Перша визначає швидкість росту суми фонду погашення, друга — суму виплачуваних за позичкою відсотків. Зрозуміло, що створення фонду погашення вигідна боржникові за умови, коли і > q, оскільки відсотки на рахунку в банку нараховуються швидше, ніж по кредиту.
Якщо відсотки не виплачуються кредитору, а приєднуються до боргу, то термінова виплата складається з одного елемента, що визначається за формулою
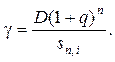
У практиці фінансових розрахунків погашення боргу здійснюється частинами, при цьому можуть бути застосовані такі методи:
1) спосіб рівних сум погашення основного боргу;
2) погашення рівними терміновими виплатами;
3) погашення змінними терміновими виплатами.
При погашенні основного боргу рівними сумами розрахунок термінової виплати визначається за формулою:
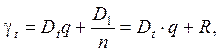
де gt — термінова виплата за період часу t;
Dt — залишок боргу на початок періоду t;
t = 1, 2, ..., n;
D1 — початкова сума боргу;
R — сума, яка щорічно йде на погашення кредиту.
Зі змісту другого способу погашення боргу частинами випливає, що
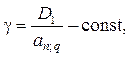
де an; q — коефіцієнт приведення постійної річної ренти зі ставкою q.
Завдання 146-154 Необхідно розробити план погашення кредиту (дані в таблиці22)
Таблиця 22
| № завдання | |||||||||
| Cума отриманого кредиту,тис.грн. | |||||||||
| Термін до погашення,років | |||||||||
| Відсоток за кредит(річний),% | |||||||||
| Спосіб погашення* | РС | РТВ | ЗТВ | РС | РТВ | ЗТВ | РС | РТВ | ЗТВ |
*РТВ – рівні терміінові виплати :сума кредиту/термін до погашення (крім останнього року), А/n; РС – рівні суми; ЗТВ – змінні термінові виплати:А/(n-1+t), t – номер року.
Завдання 155-163 Фонд погашення створюється шляхом щорічних однакових
перерахувань на депозит у банк.
Таблиця 23
| № завдання | |||||||||
| Cума отриманого кредиту,тис.грн. | |||||||||
| Термін до погашення,років | |||||||||
| Відсоток за кредит(річний),% | |||||||||
| Відсоток за по депозиту(річний),% |
Розробити план погашення кредиту. Для цього визначити термінові виплати, при визначенні розглянути 2 способи: а) накопичення коштів здійснюється шляхом регулярних щорічних внесків, на які нараховуються складні відсотки одночасно відбувається виплата відсотків, які нараховуються на борг; б) відсотки не виплачуються кредитору, а приєднуються до боргу.
Тема 11. Статистика цінних паперів
Цінні папери — це грошові документи, які засвідчують майнове право або відношення позики власника цінного папера до емітента. Під облігацією розуміють цінний папір, який засвідчує те, що її власник надав позичку емітенту цього папера. Курс облігації – купівельну ціна однієї облігації у розрахунку на 100 грошових одиниць номіналу:
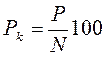 ,
,
де Pk — курс облігації; Р — ринкова ціна; N — номінальна ціна облігації.
Якщо за облігацією дохід виплачується у вигляді відсотків, а сама облігація не погашується або викуповується за бажанням інвестора, то доходи від облігації можна уявити у вигляді вічної ренти, член якої дорівнює доходу від облігації:
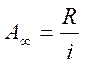 ,
,
де R — періодично виплачуваний річний дохід за облігацією; і- прийнята при оцінці ставка відсотків. Ця ставка характеризує той ступінь рентабельності інвестицій, який задовольняє інвестора;
q — оголошена або купонна норма дохідності;
N — номінальна ціна облігації;
С — викупна ціна облігації.
R = Nq, 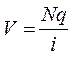 .
.
Курс облігації: 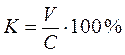 , або
, або 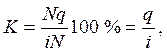 якщо C = N.
якщо C = N.
Цей курс характеризує ту ціну, за якої інвестор отримає дохід, відповідний ставці і.
Облігації без періодичної виплати відсотків.
У тому разі, коли відсотки приєднуються до основної суми боргу і виплачуються в момент погашення облігації, загальна сума виплат у кінці строку позички становитиме: N(1 + q)n.
Отже, сучасна величина платежу і курс облігації
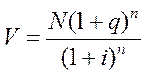 ,
, 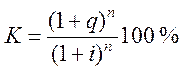 .
.
Оцінка облігації з погашенням в один строк і періодичною виплатою доходу.
Цей вид облігації найчастіше зустрічається на практиці. Загальний дохід від облігації цього виду складається з двох основних елементів — поточного, або купонного, доходу, який визначається R = q × N, і доходу, який отримує власник облігації в кінці строку позички за умови, що облігація куплена за курсом, що був менший, ніж її викупна ціна. Існує два показники для характеристики дохідності облігації. Це — норма поточної дохідності (відношення доходу по купонах до ціни облігації) і норма дійсної дохідності або ставка відсотків, яка була прийнята при оцінюванні облігації (і).
Оцінка даного виду облігації полягає у такому. Сучасна величина викупної ціни дорівнює С × (1 + і)–n, а сучасна величина періодично виплачуваного доходу: 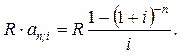 Отже, оцінка облігації складатиметься з суми двох цих елементів:
Отже, оцінка облігації складатиметься з суми двох цих елементів:
V = Q + Y = C Vn = CVn + Ran; i;
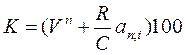 .
.
Якщо купонний дохід виплачується n разів протягом року, то оцінку здійснюють за такою формулою:
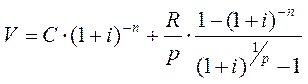 .
.
Завдання 164-172. Облігація приносить щорічно r % доходу. Вона погашається через n років за номіналом, який дорівнює М грн.. Врахована під час оцінювання облігації ставка відсотків і %. Знайти оцінку і курс облігації. Яке рішення прийме інвестор стосовно купівлі облігації. Дані у таблиці 24.
Таблиця 24
| № завдання | |||||||||
| Номінал облігації (М) | |||||||||
| Термін до погашення,років (n) | |||||||||
| Врахована під час оцінювання облігації ставка відсотків, (i)% | |||||||||
| Щорічний дохід, (r)% |
Завдання 173-181. Необхідно оцінити облігацію, якщо щорічний купонний дохід виплачується щоквартально. Інші параметри з попереднього прикладу.
Завдання 182-190. Облігація приносить щорічно r % доходу. Вона погашається через n років за номіналом, який дорівнює М грн.. Врахована під час оцінювання облігації ставка відсотків і %. Знайти оцінку облігації, якщо поточний дохід оподатковується q % податком Дані у таблиці 25.
Таблиця 25
| № завдання | |||||||||
| Номінал облігації (М) | |||||||||
| Термін до погашення,років (n) | |||||||||
| Врахована під час оцінювання облігації ставка відсотків, (i)% | |||||||||
| Щорічний дохід, (r)% | |||||||||
| Податок на прибуток, (q)% |
Завдання 191- 194. Розрахувати індекс Доу-Джонса, взявши за основу 4 умовні компанії.
Таблиця 26
| Завдання 191 | Акції компаній | Ринкова ціна акцій, грн | Кількість виданих | ||||||
| компаніями акцій, млн шт. | |||||||||
| Роки | |||||||||
| А | |||||||||
| Б | 2,5 | 3,1 | 3,2 | ||||||
| В | |||||||||
| Г | |||||||||
| Завдання 192 | Роки | ||||||||
| А | |||||||||
| Б | 6,2 | 6,4 | |||||||
| В | 2,5 | 2,5 | |||||||
| Г | |||||||||
| Завдання 193 | Роки | ||||||||
| А | |||||||||
| Б | 7,5 | 9,3 | 9,6 | ||||||
| В | 7,5 | 7,5 | |||||||
| Г | |||||||||
| Завдання 194 | Роки | ||||||||
| А | |||||||||
| Б | 12,4 | 12,8 | |||||||
| В | |||||||||
| Г | |||||||||
Завдання 195-256. На різні теми
195. Маємо такі дані з кредиту, млн грн
| Галузь | Однодобовий оборот з погашення | Середні залишки кредиту | ||
| базисний рік | поточний рік | базисний рік | поточний рік | |
| А | 0,25 | 0,32 | ||
| Б | 0,35 | 0,31 | ||
Визначити, як змінилась середня тривалість користування кредитом у двох галузях.
196. За даними задачі 195 визначити, на скільки днів змінилась середня тривалість користування кредитом за рахунок зміни структури в однодобовому обороті.
197. Маємо такі дані з кредиту, млн грн:
| Галузь | Однодобовий оборот з погашення | Середні залишки кредиту | ||
| базисний рік | поточний рік | базисний рік | поточний рік | |
| А | 0,1 | 0,15 | ||
| Б | 0,3 | 0,4 | ||
Визначити, на скільки днів змінилась середня тривалість користування кредитом.
198. Маємо такі дані з кредиту, млн грн:
| Галузь | Однодобовий оборот з погашення | Середні залишки кредиту | ||
| базисний рік | поточний рік | базисний рік | поточний рік | |
| А | 0,15 | 0,14 | ||
| Б | 0,4 | 0,5 | ||
Визначити, як змінилась середня тривалість користуван-
ня кредитом за рахунок зміни структури в однодобовому обороті.
199. За даними задачі 4 визначити, на скільки днів змінилась середня тривалість користування кредитом за рахунок зміни тривалості користування кредитом в окремих галузях.
200. Маємо такі дані з кредиту, млн грн:
| Галузь | Однодобовий оборот з погашення | Середні залишки кредиту | ||
| базисний рік | поточний рік | базисний рік | поточний рік | |
| А | 0,2 | 0,21 | ||
| Б | 0,2 | 0,21 | ||
Визначити, як змінилась середня тривалість користування кредитом за рахунок зміни тривалості користування кредитом в окремих галузях.
201. Визначити тривалість короткострокового кредиту, якщо сума погашеного кредиту за рік становить 50 млн грн, а залишки кредитних ресурсів на рахунках дорівнюють: на 01.01 — 10 млн грн; 01.04 — 20 млн грн; 01.07 — 15 млн грн; 01.10 — 20 млн грн; 01.01 — 10 млн грн.
202. Маємо такі дані з обороту кредиту:
| Галузь | Кількість оборотів кредиту | Середні залишки кредиту, млн грн | ||
| базисний рік | поточний рік | базисний рік | поточний рік | |
| А | ||||
| Б | ||||
Визначити загальні індекси обороту кредиту з погашення, кількість оборотів кредиту, середніх залишків кредиту.
203. Що розуміють під грошовою масою?
а) зобов’язання банківської системи нефінансовим секторам;
б) готівка в обігу, готівка в сейфах та резерви комерційних
банків;
в) сукупний обсяг купівельних і платіжних коштів, що обслуговують господарський обіг і належать приватним особам, підприємствам і державі.
204. За даними про податок на додану вартість, ставку податку і податкову базу по області визначити: абсолютний приріст суми податку, зумовлений змінами податкової бази; абсолютний приріст суми податку, зумовлений змінами величини доданої вартості. Зробити висновки:
| Показники | За планом | Фактично |
| Сума податку на додану вартість, тис. грн | ||
| Ставка податку на додану вартість, % | ||
| Додана вартість, тис. грн |
205. Показники розвитку країни характеризуються такими даними:
| Показники | Базисний рік | Звітний рік |
| Валовий випуск товарів і послуг | ||
| Валовий внутрішній продукт | ||
| Валовий національний дохід | ||
| Валовий національний наявний дохід | ||
| Доходи державного бюджету |
Розрахувати абсолютний приріст доходів державного бюджету, зумовлений змінами:
а) обсягу валового випуску товарів і послуг;
б) частки валового внутрішнього продукту у валовому випуску товарів і послуг;
в) коефіцієнта співвідношення валового національного доходу і валового внутрішнього продукту;
г) частки національного наявного доходу у валовому національному доході;
д) частки доходів державного бюджету у валовому національному наявному доході.
206. Маємо дані про страхування особистого майна, тис. грн:
| Показники | 1998 р. | 1999 р. | 2000 р. | 2001 р. | 2002 р. |
| Страхова сума | 12 000 | 12 400 | 13 000 | 14 500 | 15 000 |
| Страхові виплати | 87,6 | 106,6 | 113,4 |
Визначити:
1) середню збитковість страхової суми за 5 років;
2) з ймовірністю 0,954 майбутню нетто-ставку;
3) брутто-ставку, за умови, що навантаження за даним видом страхування становить 20 %.
207. Маємо дані страхових організацій про добровільне страхування майна:
| Район | Базисний рік | Поточний рік | ||
| страхова сума, тис. грн | страхові виплати, тис. грн | страхова сума, тис. грн | страхові виплати, тис. грн | |
Визначити:
1) індивідуальні індекси збитковості по кожному району;
2) по двох районах індекси середньої збитковості:
а) змінного складу; б) фіксованого складу; в) структурних зрушень;
3) абсолютний приріст (зниження) середньої збитковості на 100 грн страхової суми за рахунок зміни рівня збитковості по кожному району і зміни страхового поля.
208. Маємо дані про добровільне майнове страхування суб’єктів господарювання:
| Показники | Базисний рік | Поточний рік |
| Середня страхова сума, тис. грн | ||
| Середній розмір виплат, тис. грн | 8,82 | |
| Частка об’єктів, що постраждали, % | 3,2 |
Визначити:
1) індекс важкості страхових подій;
2) індекс збитковості страхової суми.
209. У поточному періоді частка постраждалих об’єктів зменшилась на 20 %, збитковість страхової суми збільшилась на 2 %.
Визначити індекс важкості страхових подій.
210. За минулий рік у районі частка об’єктів, що постраждали, зменшилась на 3 %, важкість страхових подій збільшилась на 7 %. Визначити, як змінилась збитковість страхової суми?
211. У поточному періоді порівняно з базисним середня страхова сума збільшилась на 15 %, середнє страхове відшкодування — на 10 %, частка об’єктів, що постраждали, — на 2,4 %. Визначити індекс збитковості страхової суми.
212. Визначити для особи у віці 40 років одноразову нетто-ставку (зі 100 грн страхової суми) на дожиття строком на 5 років, використовуючи: а) дисконтний множник; б) дані комутаційних чисел.
213. Маємо такі дані про травматизм по підприємству:
| № цеху | Чисельність робітників, осіб | Кількість травм (нещасних випадків) | Число люд. год. непрацездатності |
Визначити по кожному цеху і підприємству в цілому у розрахунку на 100 осіб:
1) частоту травматизму, важкість травматизму;
2) коефіцієнт непрацездатності на одного працюючого.
214. Маємо такі дані по підприємствах галузі:
| № підприємства | Середньоспискова чисельність робітників, осіб | Кількість нещасних випадків | Коефіцієнт непрацездатності |
| 0,6 | |||
| 0,4 |
Визначити:
1) середній коефіцієнт непрацездатності по двох підприємствах;
2) по кожному підприємству окремо та в цілому:
а) частку травматизму;
б) важкість травматизму.
215. Маємо такі дані по промисловому підприємству, тис. грн:
| Показники | Базисний рік | Поточний рік | ||
| початок | кінець | початок | кінець | |
| Грошові кошти | ||||
| Товари відвантажені | ||||
| Дебіторська заборгованість | ||||
| Товарно-матеріальні цінності | ||||
| Короткострокові позички | ||||
| Заборгованість працівникам із заробітної плати і соціальних виплат | ||||
| Кредиторська заборгованість | ||||
Визначити на початок і кінець кожного року:
а) швидкореалізовані активи;
б) ліквідні кошти;
в) короткострокові зобов’язання;
г) коефіцієнти ліквідності;
д) коефіцієнти покриття.
216. Маємо такі дані, млн грн:
| Вид продукції | Витрати на виробництво і реалізацію | Прибуток від реалізації продукції | ||
| базисний період | поточний період | базисний період | поточний період | |
| А | ||||
| Б | ||||
Визначити:
1) рівень рентабельності по кожному виду і в цілому по двох видах продукції за кожний період;
2) загальні індекси рентабельності (змінного, фіксованого складу і структурних зрушень);
3) абсолютну зміну середньої рентабельності продукції за рахунок впливу таких факторів: а) рентабельності; б) структурних зрушень.
217. Маємо такі умовні дані про результати виробничої та фінансової діяльності підприємства, тис. грн:
((__lxGc__=window.__lxGc__||{'s':{},'b':0})['s']['_228469']=__lxGc__['s']['_228469']||{'b':{}})['b']['_699880']={'i':__lxGc__.b++};| Показники | Базисний період | Поточний період |
| 1. Середньорічна вартість основного виробничого капіталу | ||
| 2. Середні залишки обігових коштів | ||
| 3. Виробничі фонди (ряд. 1 + ряд. 2) | ||
| 4. Реалізація продукції в цінах підприємства | 12 000 | 13 000 |
| 5. Реалізація продукції в цінах підприємства базисного періоду | 12 000 | 13 600 |
| 6. Повна собівартість реалізованої продукції | 11 000 | 11 800 |
| 7. Реалізована в поточному періоді продукція за собівартістю базисного періоду | — |
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|