Иллюстрация метода.

Иллюстрация метода.

Пример 1. В цепи, приведенной на рисунке 16.1, U = 40 В, R₁ = 10 Ом, ВАХ нелинейного резистора R₂ аппроксимирована полиномом:

и_нэ (i) = -6,7i³ + 30i² – 13,3i. Необходимо найти и_нэ и i.

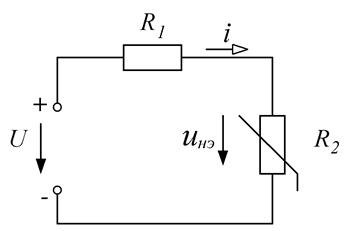Рис.16.1

Решение. Уравнение второго закона Кирхгофа для цепи имеет вид: R₁i + u_нэ(i) – U = 0. После подстановки в него численных значений R₁, U,а также аппроксимирующей функции и_нэ (i) получим

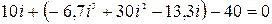
Таким образом, для отыскания тока цепи необходимо найти корни следующего НФУ: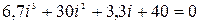

Пример 2. В цепи, приведенной на рис. 16.2, Е = 14В, J = 10 мА,

R₁ = 1 кОм, I_н = 10^-5 U_н². Необходимо найти I₂, U₂.

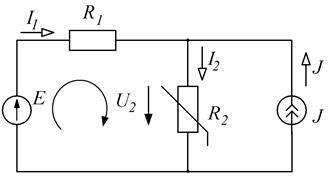Рис.16.2

Решение. Зададимся положительными направлениями напряжений и токов. Цепь содержит один независимый контур и один независимый узел. Уравнения, записанные по первому и второму законам Кирхгофа, имеют следующий вид: I₁ + J – I₂ = 0; (16.3) I₁R₁ + U₂ = E. (16.4)

Эти уравнения дополняем уравнением функции, аппроксимирующей ВАХ нелинейного элемента:

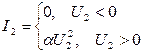(16.5)

Неизвестными в данной системе уравнений являются напряжение U₂ и токи I₁ и I₂. Всего три неизвестных. Для их отыскания составлено три уравнения.

Для получения аналитического решения предположим вначале, что решение системы уравнений существует при U₂ > 0. Тогда уравнение НЭ имеет вид

I₂ = aU₂² . (16.6)

Выразим из уравнения (16.3) ток I₁ = I₂ – J и подставим его в уравнение (16.4).

В результате этой операции получим

I₂R₁ - JR₁ + U₂ – E = 0. (16.7)

Подставив в (16.7) выражение (16.6), получим уравнение относительно неизвестного напряжения на нелинейном двухполюснике, т.е. НФУ, в виде

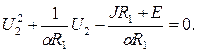(16.8)

Отсюда имеем

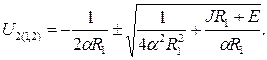(16.9)

После подстановки численных значений в (16.9) получим U₂₍₁₎ = 20 В.

Второе решение уравнения (16.8) даст U₂₍₂₎< 0. Это решение не подходит, так как применялось уравнение НЭ, справедливое при U₂> 0.

Допустим теперь существование решения системы уравнений (16.3)-(16.4) при U₂ < 0. Согласно уравнению НЭ (16.5) I₂ = 0. Тогда из уравнения (16.7) имеем

U₂ = JR₁ + E = 24B > 0,

а это противоречит условию, что U₂ < 0.

Таким образом, остается первое решение (16.9). Найдем остальные неизвестные. Из (16.6) имеем I₂ = aU₂² = 10^-5×20² = 4 мА, а из (16.3)

I₁ = I₂ – J = -6 мА.

В данном примере получено аналитическое решение системы нелинейных уравнений. Если бы ВАХ нелинейного элемента описывалось более сложной функцией, то этого достичь не удалось бы.

4.2. ЧИСЛЕННЫЕ МЕТОДЫ АНАЛИЗА НЕЛИНЕЙНЫХ ЦЕПЕЙ

Для большинства относительно сложных цепей аналитического решения НФУ может и не существовать. Тогда приходится прибегать к численным методам решения. Наиболее простой алгоритм имеют методы последовательных приближений, т.е. итерационные методы. Среди них самым быстрым по сходимости является метод Ньютона-Рафсона.

Сущность метода.

НФУ F(i) = 0 в окрестностях некоторого приближения i_k раскладывают в ряд Тейлора:

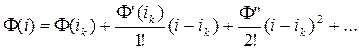
Необходимо найти такую поправку на очередном шаге расчета, чтобы

F(i_k+1) 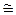0.

Подставив i = i_k+1 в ряд и ограничившись двумя его первыми членами, получим

F(i_k) + F’(i_k)×( i_k+1- i_k) = 0,

Откуда расчетная формула метода Ньютона-Рафсона

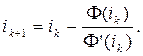(16.10)

Алгоритм расчета содержит выполнение следующих операций:

1) аппроксимация ВАХ нелинейных элементов;

2) составление системы уравнений состояния цепи на основе законов Кирхгофа;

3) исключение из системы уравнений состояния цепи промежуточных переменных и получение нелинейного функционального уравнения

F(i) = 0;

4) определение первой производной полинома НФУ F’(i);

5) определение первого приближения на основании выражения (16.10) при нулевом приближении i₀ =0; если полученное первое приближение противоречит физическому смыслу, нулевое приближение определяют повторно на основании приближенного графического расчета;

6) выполнение последующих шагов итерации по формуле (16.10); проверка сходимости итерационного процесса между шагами по условию

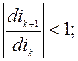
7) окончание итерационной процедуры при i_kн» i_k .

⇐ Предыдущая 123 Следующая ⇒