на встречу друг другу, на сближение появляются в учебнике

М4М ч.2 с.16.

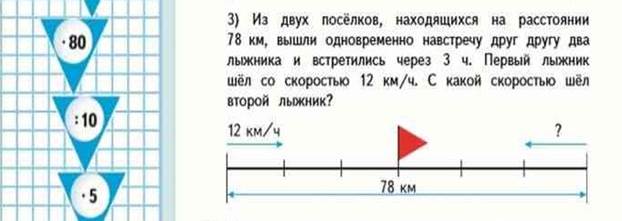
3 вид– на нахождение скорости одного из движущихся.

М4М ч.2 с.16.

б) движение в противоположные стороны, на удаление.

М4М ч.2 с.33.

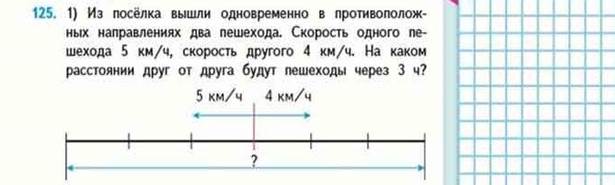
? 5 км/ч 4 км/ч ?

Аналогично предыдущему случаю разбирают, что такое скорость удаления – это расстояние, на которое удаляются движущиеся объекты за единицу времени. Она равна сумме скоростей.

Решают так же двумя способами.

1 способ 1) 5 ∙ 3=15(км) 2) 4 ∙ 3=12(км) 3) 15+12=27(км)	2 способ 1)5+4=9(км/ч) – скорость удалени 2) 9 ∙ 3=27(км)

К такой задаче составляются две обратные, на нахождение времени и скорости.

М4М ч.2 с.33.

Задачи на движение в противоположных направлениях:

- на встречу друг другу, на сближение появляются в учебнике

М4М ч.2 с.17

60 км/ч ?км/ч

520 км

Решение:

1) 60 *4=240 (км)- прошёл 1 поезд

2) 520-240=280 (км)- прошёл второй поезд

3) 280:4=70 (км/ч)- скорость 2 поезда.

М4М ч.2 с.17

?км ?км

120км

Решение:

1) 22+18=40 (км/ч) – скорость сближения

2) 120:40=3 (ч) – теплоходы были в пути

3) 22*3=66 (км) – прошёл 1 теплоход

4) 18*3=54 (км) – прошёл 2 теплоход

- в противоположные стороны, на удаление

М4ч.2 с.32

90м/мин 40м/мин

270 м ?м

Решение.

1)270:90=3 (мин) – плыл 1ый пловец

2)40*3=120 (м) – проплывёт 2ой пловец

М4Мч.2 с.34

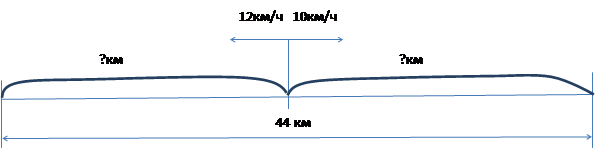
?ч ?ч

Решение.

1)12+10=22 (км/ч) – скорость удаления

2)44:22=2 (ч)- потребуется для прохождения 44км

3)12*2=24 (км) – прошёл 1 лыжник

4)10*2=20 (км) – прошёл 2 лыжник

По программе Л.Г. Петерсон знакомство с задачами на движение начинается во втором полугодии третьего класса.

М3Пч.3с.1-2

Основное внимание уделено построению формулы пути s = v ∙ t выделяют зависимые характеристики процессов, устанавливают взаимосвязи между ними и описывают их с помощью формул, таблиц и графических моделей.

М3Пч.3с.4-5

Затем даются табличные задания на взаимосвязь скорость, время, расстояние.

М3Пч.3с.5

При решении текстовых задач продолжается работа по обучению детей их самостоятельному анализу. Вводится табличный способ краткой записи условия, который используется при решении задач на формулы пути.

Построение формулы произведения позволяет провести классификацию всех изученных видов простых задач и на этой основе познакомить с общим подходом к построению алгоритмов решения составных задач, который станет для учащихся в дальнейшем надежным основанием для этого вида математической деятельности.

Решение задач на движение является традиционной темой для школьного курса математики и, в частности, для курса начальной математики. Значимость ее в данной программе определяется не только практической целесообразностью в связи с широкой распространенностью различных видов движения в повседневной жизни. Зависимости между величинами, характеризующими равномерное движение тел, допускают использование таблиц, наглядную графическую интерпретацию и потому удобны для создания общей рамки, в которую вписываются аналогичные процессы. На этой основе в дальнейшем развивается функциональное мышление детей и проводится систематизация различных видов текстовых задач, что является важнейшим этапом в обучении их решению.

Таким образом, особенностями изучения задач на движения в данном курсе являются:
1. Соотнесение зависимостей между скоростью, временем и расстоянием с графическими моделями и выражение их в буквенном виде.
2.Систематическое использование таблиц для фиксации и анализа условия текстовых задач.
3.Введение в курс задач на движение с буквенными данными.
Введение понятия скорости на 1-м уроке связано с решением проблемы о том, какая величина характеризует, быстрее или медленнее движется объект. Как обычно, обсуждение этой проблемы связывается с отработкой вычислительных навыков и повторением тех вопросов, которые учитель считает дидактически целесообразным включить в данный урок в конкретной ситуации его класса.
На 2-м уроке учащиеся строят формулу пути, устанавливающую взаимосвязь между величинами скорость, время и расстояние. Перед ними ставится задача установить взаимосвязь между величинами и записать её в виде равенства.
На 3-м уроке учащиеся продвигаются, с одной стороны, в умении строить графические модели и формулы зависимости между величинами, описывающими конкретные виды движения, а с другой — в использовании таблиц для краткой записи задач на движение и анализа условия. В зависимости от психолого-педагогических особенностей учащихся количество выполненных заданий и формы работы на уроке могут быть различными — фронтальная, индивидуальная, групповая и др.

М3Пч.3с.7-8

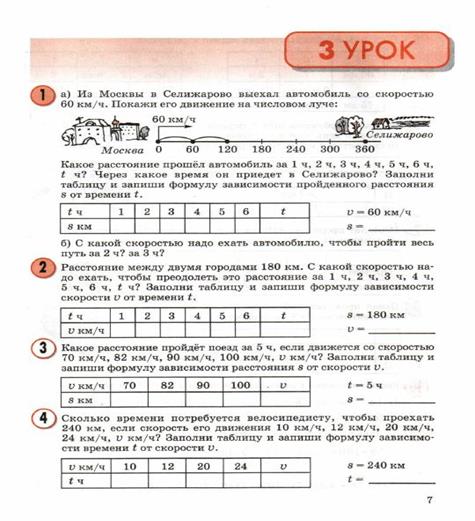
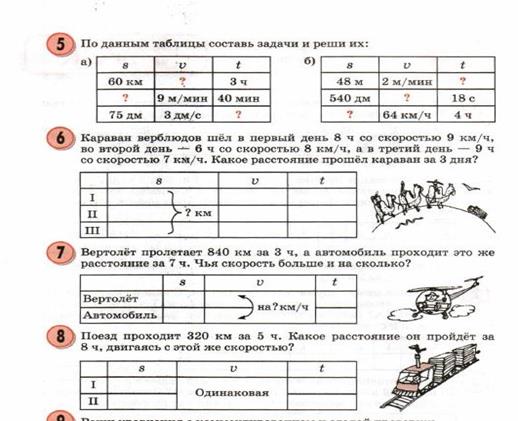
На 4-м уроке учащиеся делают следующий шаг в усвоении формулы пути. Рассматривается более сложный вид зависимости - между временем движения и расстоянием до фиксированной точки. Подобные задания чрезвычайно важны для развития функционального мышления школьников. Кроме того, здесь закладывается фундамент исследования в 4-м классе закономерностей изменения расстояния между двумя одновременно движущимися объектами и решения текстовых задач на одновременное движение двух тел.

На уроках 5 – 6 задачи на движение постепенно усложняются. Так, при построении формул зависимостей величин три различные таблицы задания предыдущего урока объединяются в одну; появляются составные задачи с буквенными данными и др. На этих уроках предполагается проведение обучающих самостоятельных работ, главная цель которых — осмысление каждым ребенком своих затруднений в изучении данной темы и, в случае необходимости, построение и осуществление проекта их исправления (работы над ошибками). Приоритетные формы работы — групповые.

М3Пч.3с.13-16

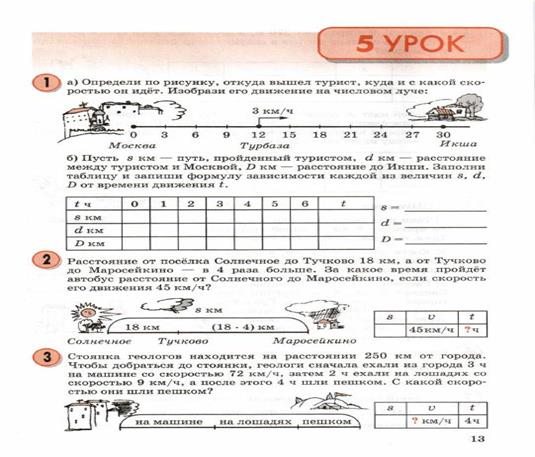
На уроках 7 – 8 тренируются и развиваются способности учащихся в решении задач на движение, сформированные на предыдущих уроках. В большинстве заданий убираются опорные схемы и таблицы: при необходимости дети должны теперь их строить самостоятельно. Способность к использованию формулы пути, в том числе и в задачах с буквенными данными, постепенно переводится в умственный план. Усложняются структуры задач. Здесь также могут широко использоваться групповые формы работы с включением игровых элементов, формы обучающего и текущего контроля, направленного на рефлексию учащимися.
М3Пч.3с.19-22

Впервые задачи на встречное движение появляются в 4 классе.

Эту задачу предлагается решить выражением.

М4Пч.2с.3

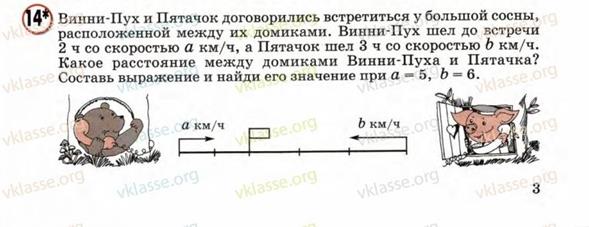
Решение.

5*2+6*3=10+18=28 (км) – между домиками Винни-Пуха и Пятачка.

Затем даются понятия и формулы скорости сближения и скорости удаления

М4Пч.2с.82

И рассматривается ряд задач по этим формулам и взаимосвязанные с ними задачи.

На встречное движение:

М4Пч.2с.83

Решение

20+16=36 (км/ч) – скорость сближения

М4Пч.2с.85

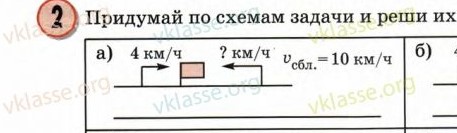
Решение

10-4=6 (км/ч) – скорость второго объекта

После отработки решения по формуле с каждым уроком задачи усложняются.

М4Пч.2 с.90

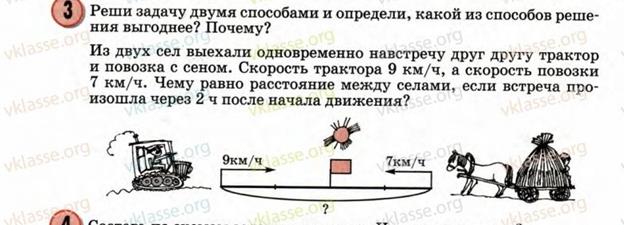
Решение

1 способ 2 способ

1)9*2=18 (км) – проехал трактор 1)9+7=16 (км/ч) – скорость сближени

2)7*2=14 (км) – проехала повозка 2)16*2=32(км) – расстояние между

3)18+14=32 (км) – расстояние между сёлами сёлами

После решения этой задачи дети должны сделать вывод, что вторым способом решать задачу выгоднее, т.к. применяя формулу сближения приходится выполнять меньше действий.

На движение в противоположных направлениях:

М4Пч.2с.83

Решение

25+32=57 (км/ч) – скорость удаления

Аналогично происходит и с задачами на движение в противоположных направлениях, после отработки решения по формуле скорости удаления. Задачи становятся более сложными.

М4Пч.2с.93

Решение

1 способ

1)80*3=240 (км) – проехал один автомобиль

2)110*3=330 (км) – проехал другой автомобиль

3)240+330=570 (км) – проехали оба автомобиля

4)570+65=635 (км) – расстояние между автомобилями через 3 часа

2 способ

1)80+110=190 (км/ч) – скорость удаления автомобилей

2)190*3=570 (км) – проехали оба автомобиля

3)570+65=635 (км) – расстояние между автомобилями через 3 часа

После решения этой задачи дети должны сделать вывод, что вторым способом решать задачу выгоднее, т.к. применяя формулу удаления приходится выполнять меньше действий.

В программе Петерсона Л.Г. формулы сближения и удаления рассматриваются на одном уроке. И отдельно выделено по уроку на рассмотрение отдельно задач на сближение и задач на движение в противоположные стороны.

⇐ Предыдущая 1 23