а) движение навстречу друг другу, на сближение

М4М ч.2 с.5-7.

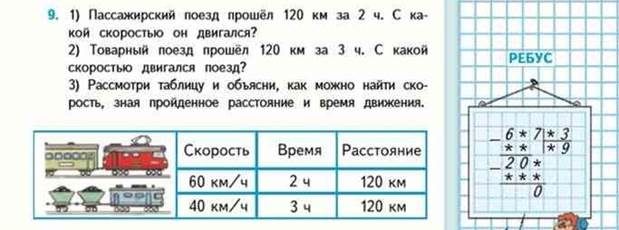
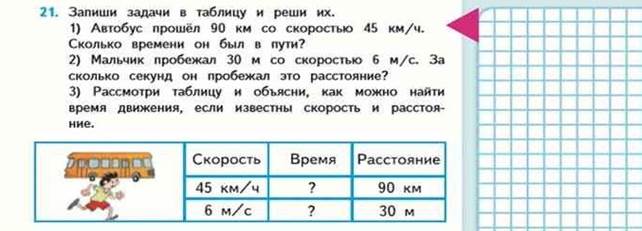
Затем эту тройку величин включают в составные задачи, сначала нетиповые.

Например: семья добиралась до озера 2 дня. В первый день они ехали на машине 4 часа со скоростью 80 км/ч, а во второй день шли пешком 2 часа со скоростью 3км/ч. Какое расстояние преодолела семья за оба дня?

Затем эти величины включают в типовые задачи.

Например, это может быть задача на нахождение 4 пропорционального или на пропорциональное деление или на нахождение неизвестного по двум разностям.

Позднее изучают специальные задачи на движение – это задачи на движение в разных направлениях и в одном направлении.

Сначала разбирают задачи на движение в разных направлениях – их два вида:

а) движение навстречу друг другу, на сближение

М4М ч.2 с.16.

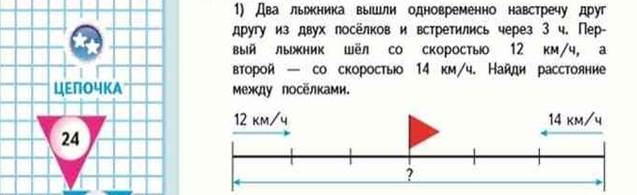
К задачам на движение можно делать таблицу. Но так же к каждой задаче можно сделать чертеж, т.е. схему со стрелками.

12 км/ч 14 км/ч

3 ч 3 ч

? ?

1 способ:

1) 12 х 3=36 (км) расстояние, пройденное 1 лыжником.

2)14 х 3=42 (км) расстояние, пройденное 2 лыжником.

3) 36+42= 78 (км) общее расстояние.

2 способ: перед введением этого способа, вводят новое понятие – «скорость сближения». Чтобы детям был понятнее смысл этого понятия можно провести драматизацию ситуации. Обсуждаем, что за каждый час лыжники сближаются на расстояние, равное сумме скоростей каждого из них – это и называется скоростью сближения.

1) 12+14=26 (км/ч) скорость сближения

(т.е. на 26 км лыжники сближаются за каждый из 3-х часов)

2)26 ∙ 3=78(км) общее расстояние

К этой задаче рассматривают еще две обратные.

2 вид– на нахождение времени движения.

⇐ Предыдущая 123 Следующая ⇒