Решим задачу.

Решим задачу.

В четверг в 9 классе пять уроков: алгебра, физика, литература, биология, химия. Сколько вариантов расписания можно составить на четверг?

Первым уроком можно поставить один из 5 предметов ( например, алгебру). Тогда вторым предметом будет один из оставшихся четверых предметов ( например, литература). И так далее. По правилу умножения мы можем посчитать варианты расписания - 5×4×3×2×1=120 вариантов.

Работа с учебником. Рассмотрите по учебнику решение задачи №6. Делаем вывод, что даже несложные задачи комбинаторики приводят к огромному числу вариантов. Становиться очевидным что все их невозможно перебрать. Но используя правило умножения легко посчитать их количество. Такие расчеты связаны с понятие факториал.

Запишите в тетрадь:

Определение. Произведение подряд идущих первых n натуральных чисел обозначают п! и называют «эн факториал» т.е. п!= 1×2×3×4×… (п-1) ×п.

Название происходит от английского математического термина factor – «сомножитель».

Так, 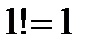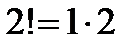, 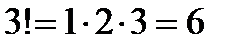. Для удобства условились считать .

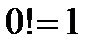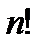растет с увеличением очень быстро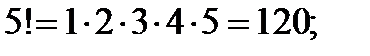

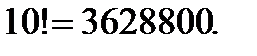
Для подсчетов удобно использовать формулы: п! = (п-1)!×п; п!= (п-2)!× (п-1)× п;

п! = 9п-3)!× (п-2) ×(п-1)× п и т.д.

Задача:

Вычислим а) 7! б) 7! 3! в) 8! × (п +1)!

6! 4! п ×(п+1) (п-1)!× 6

Решение: а) 7!= 1× 2× 3× 4× 5× 6× 7= 5040

б) 7! 3! = 6!×7×3! = 7 = 1,75

6! 4! 6!× 3! ×4 4

в) 8! × (п +1)! = 6!×7×8×(п+1)!__ = 78(п+1)! = 78 ( где п ? N и п ≥ 2)

п ×(п+1) (п-1)!× 6 (п-1)!×п(п+1)6! (п+1)!

Прочитайте по учебнику примера 7 стр. 181.

Условия задачи выглядят по - разному, но способ решения один и тот же. Значит, существует общее правило для решения задач такого типа. И оно сформулировано в виде теоремы.

Запишите в тетради:

Теорема. п различных элементов можно расставить по одному на п различных мест ровно п! способами. Р_п=п!

Буква Р соответствует первой букве английского глагола permute который переводиться как «переставлять» (перестановка). Например, Р₃=3!=6, Р₇=7!=5040.

Далее формулируем определение:

Перестановкойиз п элементов называется каждое расположение этих элементов в определенном порядке.

Обозначение: Р_п (читается «Р из п»).

Затем замечаем, что для подсчета количества перестановок можно воспользоваться комбинаторным правилом умножения, тогда

Р_п = п (п – 1) (п – 2) · … · 3 · 2 · 1

или Р_п = 1 · 2 · 3 · … (п – 2) (п – 1) · п

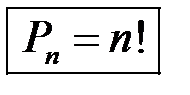
, где п! – произведение первых п натуральных чисел (читается «п факториал!»), по определению 1! = 1

Рассмотрим как факториал применяется для решения различных математических задач

Задача1. Упростим выражение 1__ - п³-п

(п-2)! (п+1)!

Решение: Сократим п³-п__ = п×(п²-1)_________ = п×(п-1)×(п+1)_____ = 1_

(п+1)! (п-2)! ×(п-1) п×(п+1) (п-2)!×(п-1)× п×(п+1) (п-2)!

1__ - 1____ =0

(п-2)! (п-2)!

2. Закрепление изученного материала

При решении задач следует особое внимание уделить анализу условий: является ли задача на комбинацию с учетом или без учета порядка элементов, как удобнее изобразить решение: с помощью дерева возможных вариантов или простым перечислением (полным перебором) или по правилу умножения.

Упражнения: № 18.1

Образец оформления решения задачи.

Решение:

а) 10×9 =90

б) 90-9= 81

в )Рассуждаем: двузначные числа из первого и седьмого десятка исключаем , так сумма цифр из которых они состоят меньше 16. Из восьмого десятка под наше условие подходит 89, из девятого десятка подходят 98 и 99 . Итого таких двузначных чисел всего три.

г) Таких двузначных чисел всего 10 ( 10,11,20,30,40,50,60,70,80,90)

№ 18.3.

Ответ:

а) 99

б) 18

в) 4×3=12

г) 40,48,80,88

№ 18.7.

Решение и ответ:

а)4×3×2=24

б) 3×2=6

в) 3×3×3=9

г)4×3=12

№ 18.11

а)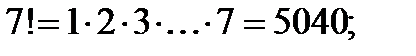

б) 8!=1× 2 ×3× 4× 5× 6× 7× 8=40 320

в) 6!-5!= 5!× 6-5!= 5!×(5-1)=5! 5=600

г)5! =1× 2× 3× 4× 5 =24

5 5

Самостоятельно выполните:

• №18.2

• №18.4

• № 18.8

• № 18.12

Спасибо за урок!!!

Фотографии выполненных заданий (вопросы по их выполнению) присылайте VK (Потапова Ольга).

⇐ Предыдущая 1 23