Временные характеристики звена

Временные характеристики звена

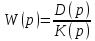Если характеристическое уравнение не имеет кратных и нулевых корней, переходная функция h(t) определяется с помощью обратного преобразования Лапласа. Если передаточную функцию представить в виде

то всоответствии с обратным преобразованием Лапласа

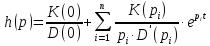
Для рассматриваемого звена i=2.

Корни характеристического уравнения

;

Рис.5.1

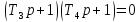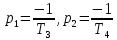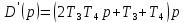Следовательно

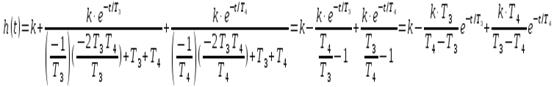
или

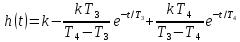
При T₃>T₄.

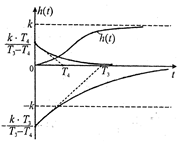
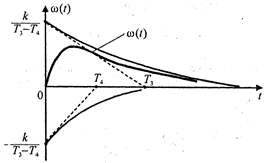
На рисунке представлены кривые переходного процесса инерционного звена 2-го порядка (его составляющие). Из графиков видно, что меньшие (малые) постоянные времени влияют на начало переходного процесса, а большие постоянные времени определяют среднюю часть и окончание процесса.

Время переходного процесса (регулирования) может быть определено

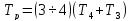Импульсная (весовая) переходная функция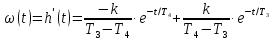

Рис.5.2

ЧАСТОТНЫЕ ХАРАКТЕРИСТИКИ ЗВЕНА

АФЧХ инерционного звена 2-го порядка имеет вид

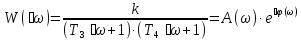Амплитудно-частотная характеристика А(ω)

Рис.5.4

Рис.5.3

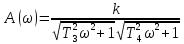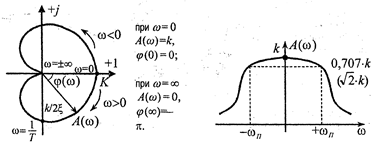
Фазо-частотная характеристика φ(ω)

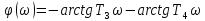Логарифмические амплитуды L(ω) и фазовой φ(ω) частотные характеристики инерционного звена второго порядка представлены:

Рис.5.5

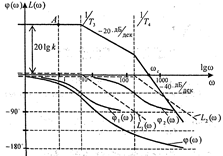
Схема АП-2 на электронных компонентах

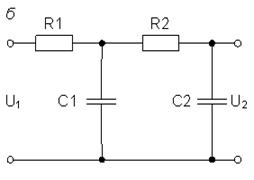
Теоретические данные.

0.55

1.924

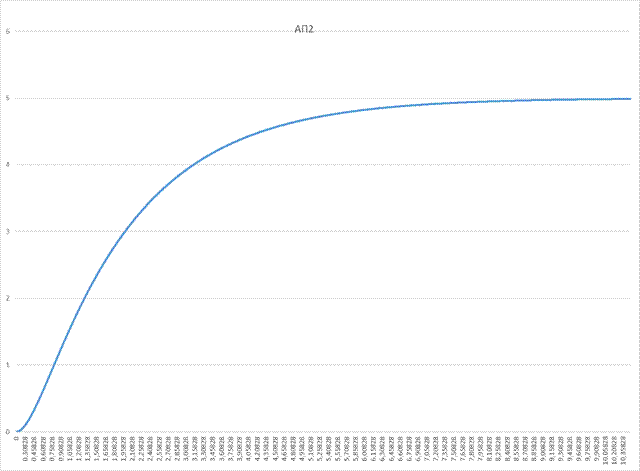
Рисунок 4.3 - «Идеальное апериодическое звено 2 порядка»

Коэффициент усиления К₀= =

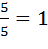
T₃=0.555

T₃+T₄=1.92

T₄=1.369

Время запаздывания τ=0.148

Передаточная функция

Практические данные.

0.295

0.13

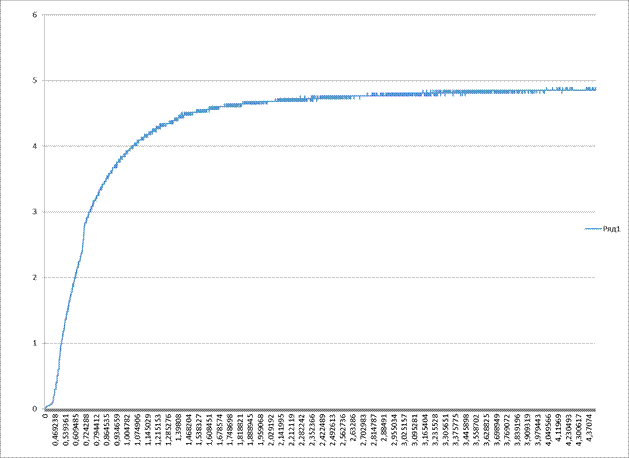
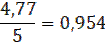
Рисунок 4.4- «Реальное апериодическое звено 2 порядка»

Коэффициент усиления К₀= =

T₃=0.13

T₃+T₄=0.295

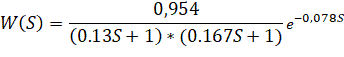T₄=0.167

τ=0.078

Передаточная функция

Вывод: Реальное звено переходит в установившейся режим быстрее, чем теоретическое. Большая разница, между постоянными времени, обуславливается не качественным соединением проводов, а также внешними факторами, такими как воздух, дополнительное сопротивление проводов, а также емкость конденсатора, индуктивность катушки индуктивности и сопротивление резисторов может быть меньше указанного.

⇐ Предыдущая 1 2 345 6 Следующая ⇒