
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
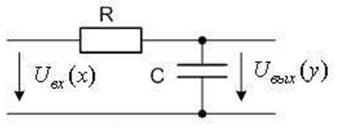
Схема АП-1 на электронных компонентах
Схема АП-1 на электронных компонентах
Теоретические данные.

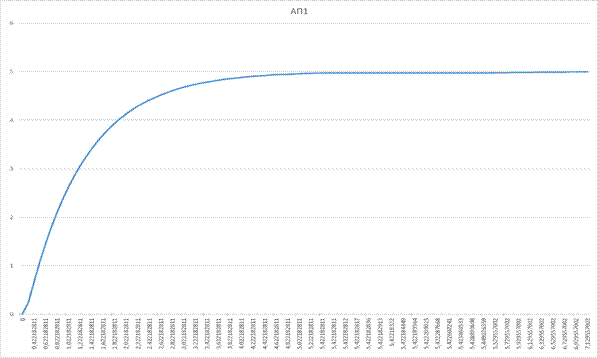
Рисунок 4.1 – «Идеальное апериодическое звено 1 порядка»
Коэффициент усиления К0= 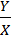 =
= 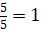
Постоянная времени T=1,02
Передаточная функция:
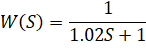
Практические данные.
|





Рисунок 4.2 – «Реальное апериодическое звено 1 порядка»
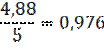 |
Коэффициент усиления К0 = 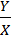 =
=
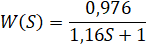 Постоянная времени T=1,16
Постоянная времени T=1,16
Передаточная функция
Вывод: реальное звено АП-1 приходит в установившееся состояние быстрее, чем теоретическое, а также имеет «шумы». В реальной модели присутствует взаимодействие внешних параметров, таких как воздух, плохое соединение проводов, а также емкость конденсатора и сопротивление резисторов может отличаться.
Апериодическое звено второго порядка
Апериодическое звено второго порядка эквивалентно двум апериодическим звеньям первого порядка, включенным последовательно друг за другом, с общим коэффициентом передачи k и постоянными времени Т3 и Т4. Пример: генератор постоянного тока. Переходный режим которого описывается дифференциальным уравнением:
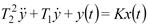
Примерами этих звеньев являются двигатель постоянного тока, если на вход его подают напряжение, а выходом является его скорость; цепочка R-L-C; генератор постоянного тока.
Операторное уравнение
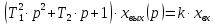 .
.
Передаточная функция
 .
.
Апериодическое звено 2-го порядка будет иметь место при последовательном соединении двух апериодических звеньев первого порядка либо при колебательном звене, если Т2>2Т1 т.к. при этом корни характеристического уравнения вещественные.
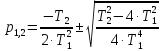 .
.
В этом случае исходное дифференциальное уравнение примет вид
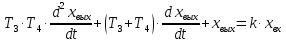 .
.
Корни характеристического уравнения
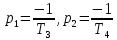 ;
;
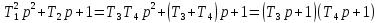 .
.
Передаточная функция звена принимает вид
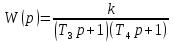 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|