
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Глава 6. Функции, непрерывные в замкнутом интервале. Правило Лопиталя ….
ОГЛАВЛЕНИЕ
| ВВЕДЕНИЕ …………………………………….…………….. | ||
| Глава 1. Элементы векторной алгебры …….......….…….. | ||
| 1. Действительные числа, числовая ось, определители второго и третьего порядков ………..…...………………………….. | ||
| 2. Декартовы координаты. Полярные координаты ………….. | ||
| 3. Векторы, линейные операции над ними …...…………..… | ||
| 4. Проекция вектора на ось …………………………………… | ||
| 5. Разложение вектора по базисным векторам …………….… | ||
| 6. Линейные операция над векторами, заданными своими проекциями ………………………………………………….… | ||
| 7. Длина вектора. Расстояние между двумя точками ………….. | ||
| 8. Направляющие косинусы векторов ……………..………… | ||
| 9. Скалярное произведение векторов, угол между векторами. Условие ортогональности двух векторов ………………….… | ||
| 10. Векторное произведение векторов, условие коллинеарности двух векторов, площадь треугольника ………………..… | ||
| 11. Смешанное произведение векторов и его геометрический смысл. Условие компланарности трех векторов …................. | ||
| Глава 2. Элементы аналитической геометрии ………........... | ||
| 1. Уравнение поверхности и уравнения линии в пространстве | ||
| 2. Плоскость, общее уравнение плоскости ………………..… | ||
| 3. Угол между двумя плоскостями, условия параллельности и перпендикулярности плоскостей ………………………….… | ||
| 4. Расстояние от точки до плоскости в пространстве …........ | ||
| 5. Прямая в пространстве и ее уравнения ……………........ | ||
| 6. Канонические уравнения прямой. Уравнения прямой, проходящей через две заданные точки …………………………… | ||
| 7. Угол между двумя прямыми, условия параллельности и перпендикулярности …………………………………….…………….. | ||
| 8. Уравнение линии на плоскости ………………………...........… | ||
| 9. Общее уравнение прямой на плоскости, угол между прямыми | ||
| 10. Уравнение прямой с угловым коэффициентом, условия параллельности и перпендикулярности прямых ……………..……. | ||
| 11. Уравнение прямой, проходящей через заданную точку с заданным угловым коэффициентом. Уравнение прямой, проходящей через две заданные точки ……………………………...…..… | ||
| 12. Кривые второго порядка. Окружность ………............……..… | ||
| 13. Эллипс ……………………………………………...………...… | ||
| 14. Гипербола …………………………………………………....… | ||
| 15. Парабола ……………………………………………………...… | ||
| 16. Преобразование координат на плоскости ….………………… | ||
| 17. Понятие о многомерном евклидовом пространстве …...….… | ||
| 18. Поверхности второго порядка. Сфера. Цилиндр ……………. | ||
| 19. Эллипсоид …………………………………………………...…. | ||
| 20. Конус ……………………………………………………..…..... | ||
| 21. Однополостный и двуполостный гиперболоиды …………… | ||
| 22. Эллиптический и гиперболический параболоиды ………...... | ||
| Глава 3. Элементы линейной алгебры ……………...……..….. | ||
| 1. Определители высших порядков ………………………….…… | ||
| 2. Свойства определителей ……………………………………….. | ||
| 3. Матрицы и действия над ними. Обратная матрица ………..… | ||
| 4. Системы | ||
| 5. Формулы Крамера ……...……………………...………….…..… | ||
| 6. Общая система линейных алгебраических уравнений. Метод Гаусса ……………….………………………………………….…. | |
| 7. Ранг матрицы. Теорема Кронекера – Капелли ……………… | |
| 8. Однородные системы ………………………….…………….… | |
| Глава 4. Теория пределов ……………………………………….. | |
| 1. Обозначения, переменные, интервалы ……….………………….. | |
| 2. Свойства абсолютной величина числа ………………………… | |
| 3. Функция. Способы задания ….............................………………. | |
4. Предел функции при 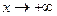 и его геометрический смысл ... и его геометрический смысл ...
| |
5. Предел функции при  и его геометрический смысл. Односторонние пределы ……..………....………………………… и его геометрический смысл. Односторонние пределы ……..………....…………………………
| |
| 6. Теоремы о пределах. Ограниченные функции …………….… | |
| 7. Бесконечно малые функции и их свойства ………………….… | |
| 8. Бесконечно большая функция, ее связь с бесконечно малой … | |
| 9. Свойства пределов ………………………….......……………… | |
| 10. Переход к пределу в неравенствах ………….……………….. | |
| 11. Первый замечательный предел ………………………………. | |
| 12. Предел последовательности. Второй замечательный предел. Натуральные логарифмы ……………............................................. | |
| 13. Сравнение бесконечно малых функций ……………………... | |
| 14. Непрерывность функции в точке и на интервале …………… | |
| 15. Свойства непрерывных функций …………………………….. | |
| 16. Точки разрыва функций ………………………………………. | |
| Глава 5. Производные функции одного переменного ………. | |
| 1. Задача об определении скорости …………..………………….. | |
| 2. Определение, механический и геометрический смыслы производной …………………………………………………………….... | |
| 3. Касательная и нормаль к кривой. Существование производной |
| 4. Дифференцируемость функции ……………..………………… | ||
| 5. Производная постоянной. Правила дифференцирования …… | ||
| 6. Производные тригонометрических и логарифмической функций ………………………………………………………………….. | ||
| 7. Производная сложной функции ………...…………………….. | ||
| 8. Производные степенной и показательной функций. Логарифмическое дифференцирование ……………………...………….… | ||
| 9. Неявная функция и её производная ………..…….…………… | ||
| 10. Обратная функция и ее производная …………..……….…… | ||
| 11. Производные обратных тригонометрических функций ……. | ||
| 12. Функция, заданная параметрически, и ее дифференцирование | ||
| 13. Дифференциал функции и его применение в приближённых вычислениях …………………………..………………………….. | ||
| 14. Производные и дифференциалы высших порядков ………... | ||
Глава 6. Функции, непрерывные в замкнутом интервале. Правило Лопиталя ……………………………………………….
1. Свойства функций, непрерывных в замкнутом интервале .......
2. Теоремы Ролля и Ферма ……………….……………………..…
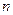 линейных алгебраических уравнений с
линейных алгебраических уравнений с