
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
ПРАВИЛА ВЫЧИСЛЕНИЯ ПОГРЕШНОСТЕЙ
ПРАВИЛА ВЫЧИСЛЕНИЯ ПОГРЕШНОСТЕЙ
подробное изложение методики измерения и расчета погрешности представлено в методических указаниях [1]. В данной работе приведены лишь основные правила вычисления погрешности при прямых и косвенных измерениях.
Бóльшая часть измерений - косвенные, а они включают в себя два различных этапа: прямые измерения и последующие расчеты. Следовательно, и оценка погрешности таких измерений также должна состоять из двух этапов. Сначала необходимо оценить погрешность значений тех величин, которые определяются непосредственно при прямых измерениях, а затем выяснить, как эта погрешность при расчетах приведет к погрешности в конечном результате.
Основной порядок математической обработки результатов многократных прямых измерений:
1) вычислить среднеарифметическое (действительное) значение измеряемой величины:
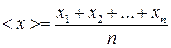 ; (П.2.1)
; (П.2.1)
2) рассчитать абсолютную погрешность прямых многократных измерений:
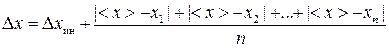 ; (П.2.2)
; (П.2.2)
3) вычислить относительную погрешность результата измерений:
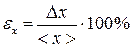 ; (П.2.3)
; (П.2.3)
4) записать окончательный результат (с учетом правила округления) в виде:
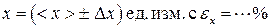 . (П.2.4)
. (П.2.4)
при записи окончательного результата измерений (и оценки погрешности) необходимо придерживаться следующего правила: значение абсолютной погрешности результата измерений округляют до двух значащих цифр слева, а среднее значение – до того разряда, в котором находится вторая значащая цифра абсолютной погрешности.
Пример. Пусть в результате измерений и расчетов было получено: 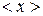 = 17,968 см и Dх = 0,237 см. Тогда окончательный результат (с учетом правил округления) следует записать в виде: х = (17,97 ± 0,24) см.
= 17,968 см и Dх = 0,237 см. Тогда окончательный результат (с учетом правил округления) следует записать в виде: х = (17,97 ± 0,24) см.
Основные этапы математической обработки результатов косвенных измерений:
1) провести прямые измерения всех величин (x, y, z, ...), входящих в рабочую формулу f = f (x, y, z, ...), и математическую обработку полученных результатов;
2) вычислить действительное (среднеарифметическое) значение измеряемой величины < f >, подставив в рабочую формулу среднеарифметические значения переменных < х >, < y >, < z >, ...:
< f > = f (< x >, < y >, < z >, ...); (П.2.5)
3) рассчитать абсолютную погрешность результата:
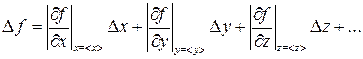 , (П.2.6)
, (П.2.6)
где 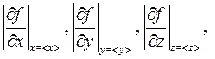 … – модули частных производных функции по переменным х, y, z, ..., вычисленные по среднеарифметическим значениям < x >, < y >, < z >, ...;
… – модули частных производных функции по переменным х, y, z, ..., вычисленные по среднеарифметическим значениям < x >, < y >, < z >, ...;
4) вычислить относительную погрешность результата:
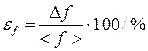 ; (П.2.7)
; (П.2.7)
5) записать окончательный результат (с учетом правила округления) в виде:
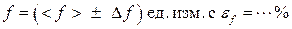 . (П.2.8)
. (П.2.8)
Если искомая величина представляет собой выражение вида
f = f(x, y, z) = xaybzc, (П.2.9)
т. е. не содержит операций сложения и вычитания, причем постоянные a, b, c могут принимать как положительные, так и отрицательные значения, проще сначала найти относительную погрешность ef:
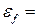
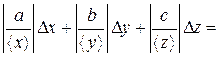 aex + bey + cez. (П.2.10)
aex + bey + cez. (П.2.10)
После этого рассчитывают абсолютную погрешность Df по формуле Df = ef×á f ñ и записывают окончательный результат в стандартном виде (П.2.8).
Если при косвенных измерениях практически невозможно воспроизвести прежние условия проведения эксперимента, то в этом случае после проведения многократных прямых измерений величин x, у, z, … для получения окончательного результата, т. е. á f ñ, Df, ef , необходимо выполнить действия в следующем порядке:
1) для каждого из значений xi, уi, zi, … вычислить значение fi косвенно определяемой величины:
fi = f(xi, yi, zi, …); (П.2.11)
2) определить среднее значение измеряемой величины:
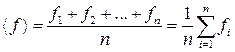 ; (П.2.12)
; (П.2.12)
3) вычислить погрешность каждого измерения:
Dfi = á f ñ - fi, i = 1, …, n; (П.2.13)
4) рассчитать случайную погрешность измерений:
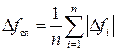 ; (П.2.14)
; (П.2.14)
5) вычислить погрешность, вносимую различными инструментами в абсолютную погрешность косвенно измеряемой величины (назовем формально эту погрешность инструментальной Dfин):
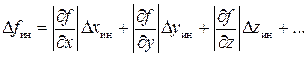 . (П.2.15)
. (П.2.15)
При этом после нахождения частных производных в полученное выражение следует подставить наименьшие из измеренных значений x, у, z, …, приводящие к наибольшей погрешности Dfин;
6) определить абсолютную погрешность:
Df = Dfсл + Dfин; (П.2.16)
7) рассчитать относительную погрешность:
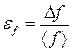 ×100 %; (П.2.17)
×100 %; (П.2.17)
8) произведя округление результатов расчета, записать окончательный результат измерения в стандартном виде (П.2.8).
Абсолютную погрешность Df косвенно измеряемой величины f можно определить без непосредственного вычисления частных производных, используя формулы численного дифференцирования (прил. 3). Полученная на основе выражения (П.2.6) формула для расчета Df примет вид:
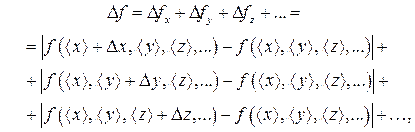 (П.2.18)
(П.2.18)
где 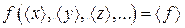 – среднее значение величины f.
– среднее значение величины f.
ПРИЛОЖЕНИЕ 3
ПРАВИЛА ДИФФЕРЕНЦИРОВАНИЯ И
ТАБЛИЦА ПРОИЗВОДНЫХ
Из определения производной вытекают несколько правил дифференци-рования, использование которых позволяет свести дифференцирование функ-ций к вычислению производных элементарных функций:
производная постоянной величины (константы) равна нулю:
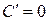 ;
;
постоянная величина (константа), являющаяся сомножителем функции, при дифференцировании выносится за знак производной:
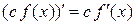 ;
;
производная суммы (разности) функций равна сумме (разности) производных функций:
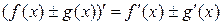 ;
;
производная произведения двух функций равна производной первой функции, умноженной на вторую, плюс произведение первой функции на производную второй:
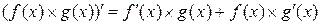 ;
;
производная частного при делении двух функций преобразовывается по формуле:
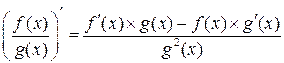 ;
;
производная сложной функции (т. е. функции от функции) равна произведению производной внешней функции по всему ее аргументу (т. е. по вложенной функции g) и производной вложенной функции по ее аргументу:
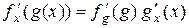
или
 .
.
(Производная сложной функции – наиболее сложное для практического применения правило дифференцирования, поэтому приведены две формы записи этого правила.)
Расчет погрешности косвенных измерений при выполнении лабораторных работ требует умения вычислять частные производные функции многих переменных. Чтобы вычислить такую производную по одному из аргументов, необходимо все остальные переменные объявить константами и руководствоваться далее обычными правилами дифференцирования:
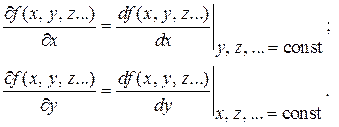
Производные некоторых наиболее часто встречающихся элементарных функций:
гармонических функций синуса и косинуса -
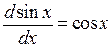 ; (П.3.9а)
; (П.3.9а) 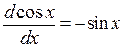 ;
;
экспоненциальной и логарифмической функций -
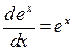 ; (П.3.10а)
; (П.3.10а) 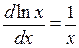 ;
;
степенной функции и два ее частных случая для n = –1 и n = 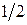 соответственно -
соответственно -
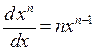 ; (П.3.11а)
; (П.3.11а)  ; (П.3.11б)
; (П.3.11б) 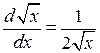 . (П.3.11в)
. (П.3.11в)
(Более полную таблицу производных можно найти в учебниках по высшей математике либо в специальных справочниках.)
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|