П.1.3. Незатухающие колебания (математический маятник)

П.1.3. Незатухающие колебания (математический маятник)

Ц е л ь р а б о т ы: изучить линейные гармонические колебания с помощью математического маятника.

П р и б о р ы и п р и н а д л е ж н о с т и: математический маятник, секундомер, измерительная линейка.

П.1.3.1. Описание установки

Математическим маятником называют идеализированную колебательную систему, состоящую из невесомой и нерастяжимой нити, на которой подвешена материальная точка.

Лабораторная установка представляет собой штатив, в верхней части которого крепится нить. К нижнему концу нити привязан металлический шарик.

П.1.3.2. Задание

Измерить длину маятника l, время t_N, _,за которое маятник совершает N полных колебаний, и определить ускорение свободного падения (напряженность гравитационного поля Земли) по формуле:

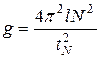. (П.1.3)

П.1.3.3. Порядок выполнения работы

1) Измерить длину l маятника от точки подвеса до центра тяжести шарика, определить инструментальную погрешность измерения длины Δl_ин и записать результаты измерения в табл. П.1.2.

2) Отклонить маятник от положения равновесия на расстояние не более 10 % от длины маятника (в этом случае колебания маятника можно считать линейными и гармоническими). Отпустить маятник и измерить с помощью секундомера время t_N совершения маятником N колебаний (N задается преподавателем). Измерения провести многократно. Результаты измерений t_N и N и инст-рументальную погрешность Δ t_N_ин секундомера записать в табл. П.1.2.

Т а б л и ц а П.1.2

Результаты измерения

при определении ускорения свободного падения

l, м	Δl_ин, м	N	t_N, c	Δt_N_ин, c

3) Сделать оценочный (приблизительный) расчет ускорения свободного падения в гравитационном поле Земли по формуле (П.1.3) и результаты измерений и расчетов подписать у преподавателя.

4) Выполнить математическую обработку результатов измерений.

5) Записать окончательный результат (с учетом правил округления).

6) Сравнить полученный результат с табличным значением ускорения свободного падения и сделать вывод.

⇐ Предыдущая 12 13 14 15 161718 19 20 21 Следующая ⇒