- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Системы и совокупность неравенств, двойное неравенство.
Системы и совокупность неравенств, двойное неравенство.
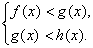
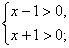
 система равносильна неравенству х > 1
Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, т.е.
Ответ.
система равносильна неравенству х > 1
Решением системы неравенств будет пересечение решений неравенств системы, т.е. промежуток, на котором обе штриховки совпали, т.е.
Ответ. 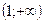
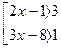
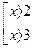
| |
| |

Решением совокупности неравенств будет объединение решений неравенств совокупности, т.е. промежуток, на котором имеется хотя бы одна штриховка, т.е.
Ответ. 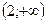
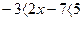 Запишем равносильную систему неравенств
Запишем равносильную систему неравенств 
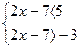
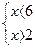
 Ответ.
Ответ. 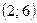
| |
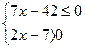
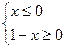
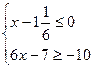
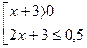
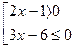
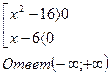

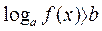 (1)
(1)
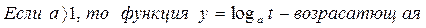 Неравенство (1) равносильно системе неравенств
Неравенство (1) равносильно системе неравенств
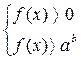 (2)
Неравенство (1) и система неравенств (2) имеют одно и то же множество решений.
Отметим решения на числовой прямой.
Ответ: (числовой промежуток)
(2)
Неравенство (1) и система неравенств (2) имеют одно и то же множество решений.
Отметим решения на числовой прямой.
Ответ: (числовой промежуток)
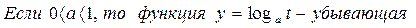 Неравенство (1) равносильно системе неравенств
Неравенство (1) равносильно системе неравенств
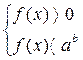 (2)
Неравенство (1) и система неравенств (2) имеют одно и то же множество решений.
Отметим решения на числовой прямой.
Ответ: (числовой промежуток)
(2)
Неравенство (1) и система неравенств (2) имеют одно и то же множество решений.
Отметим решения на числовой прямой.
Ответ: (числовой промежуток)
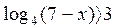
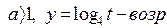
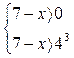
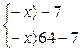

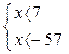

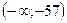

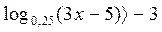
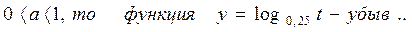 Знак!
Знак!
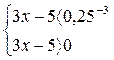
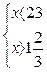
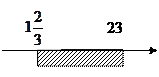 Ответ:
Ответ: 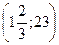
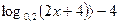 2.
2. 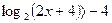 3.log0,5(2x+5) ≥−2
3.log0,5(2x+5) ≥−2