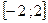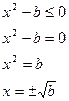- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Общие методы решения неравенств
Общие методы решения неравенств
Решением неравенства, называется всякое значение переменой, при котором данное неравенство верно. Задание "решить неравенство" означает, что требуется найти множество всех его решений. Ответ записать промежутком.
Процесс решения неравенства заключается в основном в замене данного неравенства (или данной системы неравенств) другими равносильными1. При решении неравенств применяются следующие основные приемы
1. Замена одного выражения другим, тождественно ему равным.
2. Перенос слагаемого из одной части неравенства в другую с заменой знака на противоположный
3. Умножение или деление обеих частей неравенства на одну и ту же числовую величину (не равную нулю). При этом если множитель положителен, то знак неравенства остается тем же, если же отрицателен, то знак неравенства меняется на противоположный
Каждое их этих преобразований дает неравенство, равносильное исходному.
Квадратные неравенства
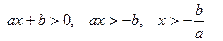
 Ответ:
Ответ: 
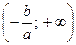
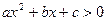
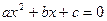
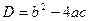
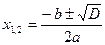

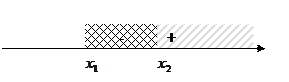 Ответ:
Ответ: 
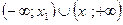
|

Ответ: 
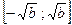
 Ответ:(4;+∞)
Ответ:(4;+∞)
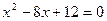 ;
; 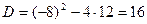
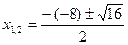
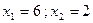
 Неравенство строгое, поэтому 2 и 6 включается в промежуток:
Ответ.
Неравенство строгое, поэтому 2 и 6 включается в промежуток:
Ответ. 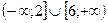

 -
Ответ:
-
Ответ: