Задача 1. Задача 2. Задача 3. Задача 4. Задача 5. Задача 6. Задача 7. Задача 8. Задача 9. Задача 10

Стр 1 из 3Следующая ⇒

Задача 1

Выяснить, какие из совокупностей многочленов степени не выше n над полем F образуют линейное векторное пространство.

а) многочлены, имеющие корень в заданных двух точках 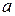и ;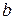

б) многочлены, у которых сумма всех коэффициентов равна нулю.

В случае положительного ответа найти размерность и базис.

Задача 2

Найти размерность суммы и пересечения подпространств, натянутых на системы векторов 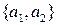и : .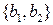

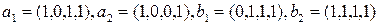Задача 3

Доказать, что сумма подпространств L и М векторного пространства V равна пересечению всех подпространств, содержащих и L, и М.

Задача 4

Найти число всех базисов 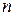-мерного пространства V над полем из 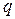элементов, содержащих заданный ненулевой вектор.

Задача 5

Является ли подпространством линейного векторного пространства многочленов от одной переменной над полем :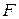

а) множество всех многочленов не содержащих четных степеней переменной ;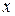

б) множество многочленов четной степени?

Задача 6

Пусть размерность суммы двух подпространств на единицу больше размерности их пересечения. Что можно сказать об этих подпространствах?

Задача 7

Пусть 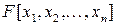--- множество многочленов от 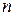переменных над полем 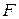. Какова размерность подпространства этого пространства, состоящего из однородных многочленов степени ?

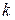Задача 8

Пусть U, V, W - подпространства векторного пространства. Докажите, что .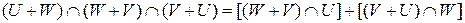

Задача 9

Пусть V - векторное пространство размерности 4 над полем из пяти элементов. Сколько существует вырожденных операторов из V в V?

Задача 10

Пусть оператор А действует на множестве квадратных матриц размерности 2 умножением на фиксированную матрицу размера 2. Найти матрицу этого оператора в пространстве всех квадратных матриц размерности 2.

12 3 Следующая ⇒