КОНТРОЛЬНЫЙ ПРИМЕР. Задание. Этапы обработки данных

2. КОНТРОЛЬНЫЙ ПРИМЕР

Задание

Имеются данные о размере заработной платы рабочих комплексной бригады (см. таблицу 2.1). Исследовать исходные данные, применив метод группировок с равными интервалами. Произвести расчет основных характеристик полученного ряда распределения. Объяснить полученные результаты. Построить гистограмму, полигон и кумуляту распределения. Найти моду и медиану графическим способом.

Таблица 2.1-Данные о размере заработной платы 30 рабочих комплексной бригады, ден.ед.

Этапы обработки данных

1. Построение интервального вариационного ряда.

Исходные данные располагают в виде первичного ранжированного дискретного вариационного ряда (см. таблицу 2.2).

Таблица 2.2- Первичный ранжированный дискретный вариационный ряд

Используя метод равных группировок (интервалов), переходят от дискретного вариационного ряда к интервальному, определив количество групп (интервалов) по формуле Стерджесса (1.1):

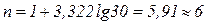Из формулы (1.2)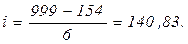

После разбивки диапазона значений варьирующего признака на интервалы определяется количество данных, попавших в каждый из них.

Для дискретного ряда, приведенного в таблице 2.2, интервальный вариационный ряд представлен в таблице 2.3 (см. 1 и 4 столбцы).

Таблица 2.3 –Группировка работников по заработной плате

Группы работников по з/п	Значение заработной платы, ден.ед, ( )	Середина интервала, ден.ед., (Х)	Количество рабочих, чел., (f)	Хf*

154,00-294,83	154, 201, 214,	224,415		673,245
294,83-435,66	302, 320, 320, 324, 325, 329, 357	365,245		2556,715
435,66-576,49	478, 517, 548, 558	506,075		2024,300
576,49-717,32	605, 615, 658, 658, 698	646,905		3234,525
717,32-858,15	745, 754, 754	787,735		2363,205
858,15-999,00	865, 896, 875, 878, 950, 968, 985, 999,	928,575		7428,600
итого	Х	Х		18280,590

2. Расчет числовых характеристик интервального вариационного ряда.

Используя формулы (1.3-1.5), рассчитывают частости и плотности распределений по группам. Результаты заносят в дополнительную таблицу 2.4 (см. 5, 6, 7 столбцы).

Таблица 2.4 (дополнительная) – Группировка работников по заработной плате

Группы работников по з/п	Середина интервала, ден.ед., (Х)	Количество рабочих, чел., (f)	Накопленная частота, чел., (S)	Частость,% (w)	Плотность абсолютная, ( 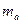)	Плотность относительная, ( )

154,00-294,83	224,415			10,0	0,0213	0,00071
294,83-435,66	365,245			23,3	0,0497	0,00166
435,66-576,49	506,075			13,3	0,0284	0,00095
576,49-717,32	646,905			16,7	0,0355	0,00118
717,32-858,15	787,735			10,0	0,0213	0,00071
Продолжение таблицы 2.4

858,15-999,00	928,575			26,7	0,0568	0,00189
итого	Х		Х	100,0	Х	Х

Среднюю заработную плату рассчитывают по формуле (1.6), с использованием промежуточных расчетов в таблице 2.3 (см. 5 столбец):

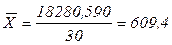(ден.ед.).

Моду и медиану для интервального вариационного ряда рассчитывают по формулам (1.7-1.8), определив предварительно модальный и медианный интервалы. Модальный интервал-(858,15-999,00), т.к. частота этого интервала (f=8) максимальная. Медианный интервал-(576,49-717,32), т.к. накопленная частота этого интервала впервые превышает полусумму всех частот ряда распределения (S=19, ).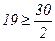

Тогда:

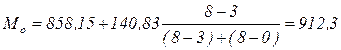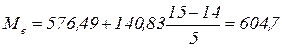(ден.ед).

Межгрупповую дисперсию 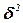найдем табличным способом (см. таблицу 2.5), воспользовавшись формулой (1.10).

Таблица 2.5-Расчетные значения для вычисления межгрупповой дисперсии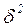

Группы		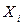Х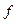

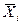
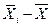
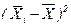
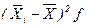
154,00-294,83	154, 201, 214	224,415	189,67	-419,73	176173,3	528519,9
294,83-435,66	302, 320, 320, 324, 325, 329, 357	365,245	325,29	-284,11	80718,5	565029,5
435,66-576,49	478, 517, 548, 558	506,075	525,25	-84,15	7081,2	28324,8
576,49-717,32	605, 615, 658, 658, 698	646,905	646,80	37,40	1398,8	6994,0
Продолжение таблицы 2.5

717,32-858,15	745, 754, 754	787,735	751,00	141,60	20050,6	60151,8
858,15-999,00	865, 896, 875, 878, 950, 968, 985, 999,	928,575	927,00	317,60	100869,8	806958,4
итого	Х	Х	Х	Х	Х	1995978,4

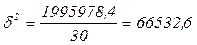Для расчета внутригрупповых дисперсий по группам воспользуемся формулой (1.11):

;

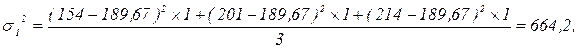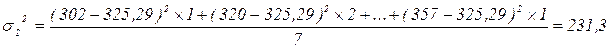аналогично рассчитываем: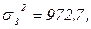

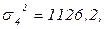
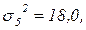
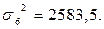
Вычислим среднюю из внутригрупповых дисперсий, используя формулу (1.12):

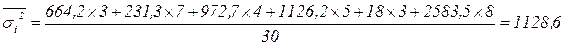По правилу сложения дисперсий (см. формулу 1.13):

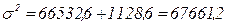Используя формулы (1.14-1.15), найдем коэффициент вариации:

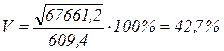Долю вариации результативного признака под влиянием факторного вычислим с помощью эмпирического коэффициента детерминации (см. формулу 1.16): 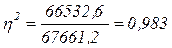(или 98,3 %).

Теснота связи между группировочным и результативным признаками (показатель Пирсона) (см. формулу 1.17):

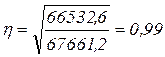3. Графическое изображение интервального вариационного ряда.

а)

б)

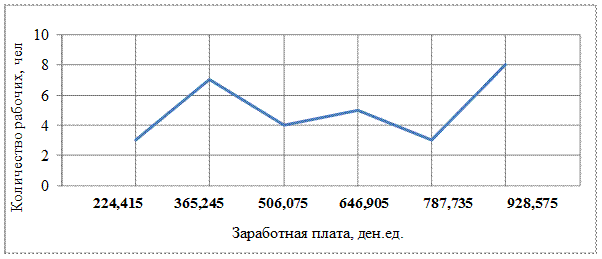в)

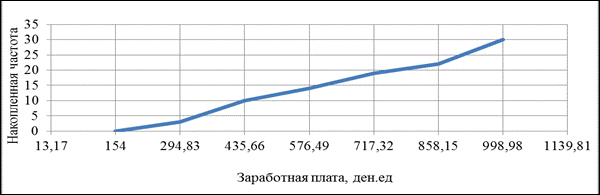
Рисунок 3.1- Распределение заработной платы по числу рабочих бригады:

а) гистограмма,

б) полигон,

в) кумулята

Абсцисса точки А (см. рисунок 3 (а)) является модой распределения. Абсцисса точки Б (см. рисунок 3 (в))- медиана распределения.

4. Экономическая интерпретация результатов статистической обработки данных.

Таким образом, исследовав информацию о заработной плате у рабочих комплексной бригады с помощью простейших статистических методов, можно сделать следующие выводы по полученным числовым характеристикам:

1) Разброс заработной платы достаточно значителен (т.е. разница между максимальным и минимальным значениями совокупности): от
154 (ден.ед.) до 999 (ден.ед.). Очевидно, что это связано с различием в квалификации рабочих комплексной бригады.

2) Размер средней заработной платы одного рабочего, являющийся обобщенной характеристикой заработных плат каждого рабочего в совокупности, равен 609,4 (ден.ед.).

3) Приблизительное значение медианы 604,7 (ден.ед) получилось ниже (604,7<609,4) этого значения. Это говорит о том, что половина всех сотрудников работают с заработной платой чуть ниже средней.

4) Наиболее часто встречающаяся заработная плата, определенная с помощью моды, приблизительно равна 912,3 ден.ед.

5) Коэффициент вариации больше 33% (42,7%), поэтому совокупность количественно неоднородная, а величина средней заработной платы на одного рабочего нетипичная.

6) Общая дисперсия, отражающая суммарное влияние всех возможных факторов (стаж работы, квалификация, характер работы, болезни и т.д.) на общую вариацию средней зарплаты всех рабочих бригады равна 67661,2.

7) Межгрупповая дисперсия характеризует вариацию групповых средних, обусловленную различиями групп рабочих по квалификации, и равна 66532,6.

8) Внутригрупповые дисперсии показывают вариации заработной платы в каждой группе, вызванные всеми возможными факторами, кроме различий в квалификации. Средняя из внутригрупповых дисперсий равна 1128,6.

9) Эмпирический коэффициент детерминации равен 98,3%. Это означает, что на 98,3% вариация в совокупности обусловлена различиями в квалификации (а, следовательно, и в заработной плате) у рабочих и на
1,7% - влиянием прочих факторов.

10) Эмпирическое корреляционное отношение равно 0,99. Это значит, что сила связи между квалификацией (группировочным признаком) и заработной платой (результативным признаком) весьма тесная.

Т.к. исследование совокупности проводилось с использованием метода равных группировок, то такие характеристики как абсолютная и относительная плотности распределения рассчитываются лишь как основные характеристики интервального вариационного ряда распределения без дальнейшего их применения.

⇐ Предыдущая 1 234 5 Следующая ⇒