ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

1. ТЕОРЕТИЧЕСКАЯ ЧАСТЬ

Для изучения предмета статистики разработаны и применяются специфические приемы, совокупность которых образует методологию статистики (методы массовых наблюдений, группировок, обобщающих показателей, динамических рядов, индексный метод и др.). Применение в статистике конкретных методов предопределяется поставленными задачами и зависит от характера исходной информации. Комплексность (системность) использования статистических методов обусловлена сложностью процесса экономико- статистического исследования, состоящего из трех основных стадий: первая- сбор первичной статистической информации, где применяется метод массового статистического наблюдения; вторая - статистическая сводка и обработка первичной информации методом статистических группировок; третья- обобщение и интерпретация статистической информации, при изучении которой широкое применение имеют табличный и графический методы.

Статистические данные, обладающие некоторыми общими свойствами, характеризующие какое-либо массовое явление принятые к обработке, называются статистической совокупностью.

В расчетно – графическом задании студентам необходимо исследовать предложенную совокупность, представив данные в компактном, обозримом виде, применив метод группировок с равными интервалами, на основе которого рассчитываются и сравниваются сводные показатели по группам, анализируются причины различия между группами, изучаются взаимосвязи между признаками и закономерности развития.

Исследование статистической совокупности проводится по следующим этапам:

1-построение интервального вариационного ряда;

2-расчет числовых характеристик интервального вариационного ряда;

3-графическое изображение интервального вариационного ряда (гистограмма, полигон, кумулята);

4-экономическая интерпретация результатов статистической обработки данных.

1 этап-построение интервального вариационного ряда

Имеющиеся в распоряжении исследователя исходные данные располагают в виде ранжированного дискретного вариационного ряда (т.е. ряда распределения, построенного по количественному признаку, в котором варианты (значения признаков) – целые числа). Он представляет собой таблицу, в которой показатели располагаются в порядке возрастания (или убывания) значений и называется первичным рядом распределения. Далее, используя метод равных группировок, переходят от дискретного вариационного ряда к интервальному вариационному ряду распределения (ряду распределения, построенному по количественному признаку, в котором варианты даны в виде интервалов и могут принимать в этих интервалах любые значения).Число групп или интервалов (n) определяется по формуле 1.1, американского ученого Стерджесса (стандартизированный подход):

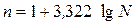, (1.1)

где n-число групп,

N- количество единиц всей совокупности.

Для группировок с равными интервалами размер интервала (i) определяется по формуле 1.2:

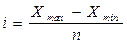, (1.2)

где X_max – наибольшее значение варьирующего признака;

X_min - наименьшее значение варьирующего признака.

Если в результате деления получается дробное число, округление производят в большую сторону (это делается для того, чтобы максимальное значение совокупности X_max попало в последний интервал).

Прибавляя к наименьшему значению признака найденное значение интервала, получаем верхнюю границу первой группы; прибавляя далее величину интервала к верхней границе первой группы, получаем верхнюю границу второй группы и т.д., пока наибольшее значение признака не окажется либо равным, либо несколько меньше значения верхней границы последней группы. Определив частоты (количество вариантов, попавших в каждую группу), получим интервальный вариационный ряд. В случае совпадения варианта со значением границы интервала (т.е. в случае неопределенности отнесения значения признака к тому или иному интервалу), используют принцип единообразия: левое число интервала включает в себя обозначенное значение, а правое – не включает, т.е. данный вариант переходит в следующий интервал.

2 этап-расчет числовых характеристик интервального вариационного ряда.

Для правильного представления о характере распределения, студентам необходимо рассчитать следующие числовые характеристики интервального вариационного ряда:

1. Частости (w) по всем группам.

2. Абсолютную ( 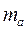) и относительную ( 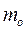) плотности распределения по всем группам.

3. Среднее значение признака ( ).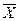

4. Медиану Me.

5. Моду Mo.

6. Общую дисперсию 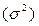, межгрупповую дисперсию 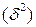,внутригрупповую дисперсию .

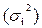7. Среднее квадратическое отклонение ( ).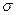

8. Коэффициент вариации (V).

9. Эмпирический коэффициент детерминации( ).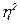

10.Эмпирическое корреляционное отношение ( ).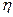

Дадим определение этих понятий и приведем формулы 1.3, расчета данных показателей.

Частость (w) -частота, выраженная в долях единиц или в процентах к итогу. (Сумма частностей равна 1 или 100%):

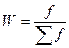, (1.3)

где f - частота.

Сумма всех частот равна численности всей совокупности.

Абсолютная плотность распределения ( 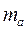)-частота, отнесенная к ширине интервала, формула 1.4:

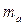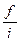= . (1.4)

Относительная плотность распределения ( 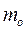) -частость, отнесенная к ширине интервала, формула 1.5:

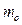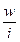= . (1.5)

Расчет абсолютной и относительной плотности распределения обычно производится для вариационного ряда с неравными интервалами. Эти показатели используют для перегруппировки данных с целью получения сопоставимых интервалов и дальнейшего их анализа.

Средней величиной ( 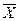) называют статистический показатель, который дает обобщенную характеристику варьирующего признака единиц однородной совокупности. Под качественной однородностью единиц совокупности понимается сходство единиц (объектов, явлений) по каким-либо существенным признакам, но различающихся по каким- либо другим признакам.

При нахождения средней величины в интервальном ряду распределения, истинные значения признака заменяются центральными (серединными) значениями интервалов, которые отличаются от средней арифметической значений, включенных в интервал. Вычисления производят по формуле 1.6 средней арифметической взвешенной:

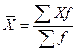, (1.6)

где Х-центральные значения интервалов.

Медиана - это вариант, находящийся в середине ранжированного вариационного ряда.

В интервальном вариационном ряду распределения медиана определяется после предварительного нахождения медианного интервала, т.е. интервала, накопленная частота которого (кумулятивная частота) равна или впервые превышает полусумму всех частот ряда по формуле 1.7:

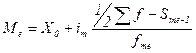, (1.7)

где Х₀ – начальное значение интервала, содержащего медиану;

i_m - величина медианного интервала;

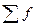- сумма частот ряда;

S_me_-1 –накопленная частота интервала, предшествующего медианному;

f_m_е – частота медианного интервала.

Мода -наиболее часто встречающийся вариант дискретного ряда распределения, т.е. вариант, имеющий наибольшую частоту.

В интервальном ряду распределения приблизительной модой считают центральный вариант так называемого модального интервала, т.е. интервала, имеющего наибольшую частоту или частость. В этом случае мода определяется (формула 1.8) так:

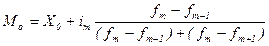, (1.8)

где Х₀ –нижняя граница модального интервала;

i_m - величина модального интервала;

f_m - частота модального интервала;

f_m_-1 – частота интервала, предшествующего модальному;

f_m₊₁ – частота интервала, следующего за модальным.

Общая дисперсия 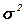измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию, и вычисляется по формуле:

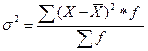. (1.9)

Межгрупповая дисперсия 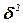- характеризует систематическую вариацию результативного признака, обусловленную влиянием признака- фактора, положенного в основание группировки, формула 1.10.

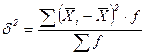, (1.10)

где 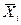- групповые средние;

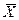- общая средняя,

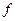- численность единиц в i-той группе.

Внутригрупповая дисперсия 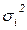-дисперсия в пределах каждой группы, которая отражает случайную вариацию, т.е. часть вариации, обусловленную влиянием неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки, формула 1.11:

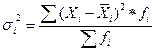, (1.11)

где 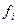- частота варианта ,

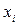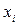-варианты внутри групп.

На основании внутригрупповой дисперсии по каждой группе можно определить общую среднюю из внутригрупповых дисперсий, формула 1.12:

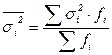, (1.12)

где 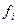- численность единиц в i-той группе.

Согласно правилу (формула 1.13) сложения дисперсий:

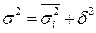. (1.13)

Использование центральных значений интервалов для вычисления общей средней 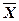заданного распределения приводит к систематической погрешности при расчете общей и межгрупповой дисперсий. В силу этого равенство между значениями 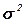, определяемыми по формулам (1.9) и (1.13) будет приблизительным. Поэтому в расчетно-графическом задании студентам необходимо вычислять общую дисперсию, используя только формулы (1.10-1.13).

При расчете дисперсии не указываются единицы измерения.

Среднее квадратическое отклонение ( 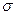) - это обобщающая характеристика размеров вариации признака в совокупности, оно показывает, на сколько в среднем отклоняются конкретные варианты от их среднего значения и выражается в тех же единицах, что и варианты, формула 1.14:

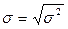. (1.14)

Чем меньше значение дисперсии и среднего квадратического отклонения, тем однороднее (количественно) совокупность и тем более типичной будет средняя величина

Коэффициент вариации (V)-выраженное в процентах отношение среднего квадратического отклонения к средней, формула 1.15:

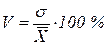. (1.15)

Коэффициент вариации используют для сравнительной оценки вариации различных признаков в одной совокупности; для сравнений колеблемости одного и того же признака в нескольких совокупностях; для характеристики однородности совокупности.

Если коэффициент вариации меньше 33%, то это значит, что совокупность количественно однородна, а средняя для нее типична.

Эмпирический коэффициент детерминации( 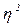)-показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации, формула 1.16:

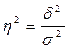. (1.16)

При отсутствии связи 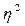=0, а при функциональной связи 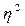=1.

Эмпирическое корреляционное отношение ( 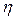)- (показатель Пирсона)-показывает тесноту связи между группировочным и результативным признаками, формула 1.17.

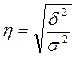. (1.17)

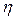принимает значения от 0 до 1.

Если связь отсутствует, то 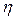=0,т.е. все групповые средние будут равны между собой, межгрупповой вариации не будет.

Если связь функциональная, то корреляционной отношение будет равно единице. В этом случае 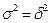, т.е. внутригрупповой вариации не будет.

Чем значение корреляционного отношения ближе к единице, тем теснее, ближе к функциональной зависимости связь между признаками (см. таблицу 1.1).

Таблица 1.1- Сила связи в зависимости от значения показателя Пирсона(соотношения Чэддока)

Значения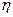	Сила связи
0,1-0,3	слабая
0,3-0,5	умеренная
0,5-0,7	заметная
0,7-0,9	тесная
0,9-0,99	весьма тесная

3-этап графическое изображение интервального вариационного ряда.

Графические методы в статистике являются способом наглядного изображения результатов статистической сводки и обработки массового материала. На этом этапе студентам необходимо проанализировать полученный ряд распределения, построив гистограмму, полигон и кумуляту.

Гистограмма распределения применяется чаще всего для изображения интервальных рядов. Для ее построения по оси абсцисс откладываются интервалы признака, а по оси ординат - численности единиц совокупности. На отрезках, изображающих интервалы, строят прямоугольники, площади которых пропорциональны численностям единиц.

Полигон строят в основном для изображения дискретных рядов. При его построении на оси абсцисс откладываются значения варьирующего признака, а на оси ординат - абсолютные или относительные численности единиц совокупности (частоты или частости). При построении полигона для интервального ряда переходят к дискретному ряду, заменяя интервалы центральными (серединными) значениями варьирующего признака.

При построении кумуляты значения варьирующего признака откладываются на оси абсцисс, а на оси ординат помещаются накопленные итоги частот или частостей. При построении кумуляты интервального ряда распределения нижней границе первого интервала соответствует частота, равная нулю, а верхней – накопленная частота данного интервала; нижней границе второго интервала соответствует накопленная частота первого интервала, а верхней- накопленная частота второго интервала и т.д.

⇐ Предыдущая 123 4 5 Следующая ⇒