Арктангес. Решение уравнения tgx = а

Стр 1 из 5Следующая ⇒

Арктангес. Решение уравнения tgx = а

Тригонометрический круг тангенса. Линия тангенсов.

Тангенс и котангенс острого угла прямоугольного треугольника определяется так:

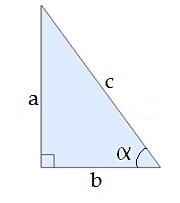
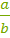ctg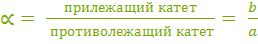

Существует наглядная и очень полезная геометрическая интерпретация тангенса с помощью так называемой линии тангенсов. Линия тангенсов – это касательная l к единичной окружности в точке А (1;0). За положительное направление линии тангенсов берут направление снизу вверх.

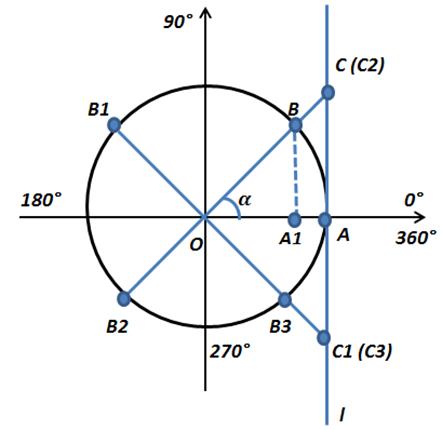
По определению тангенса угла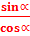(tg α =

) tg α=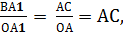

так как ОА=1. Т.е. тангенс угла α – это величина отрезка АС на линии тангенсов. tg α =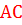

Иначе говоря, тангенс угла – это величина отрезка касательной, проведенной через точку А (конец неподвижного радиуса), от точки касания А до пересечения с продолжением подвижного радиуса ОВ. Значения тангенса читаются с оси ОУ Рассмотрим изменение величины (отрезка АС) при движении подвижного радиуса ОВ по окружности и увеличении угла. Заметим, что значение совпадают I и III квадрантах, во II и IV квадрантах:

Решим уравнение tgx =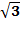

Проиллюстрируем решение уравнения на числовой окружности.

На оси тангенсов отложим отрезок, длина которого равна 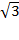и проведем через конец этого отрезка и начало координат прямую. Эта прямая пересекает еденичную окружность в двух диаметрально противоположных точках. Эти точки получены в результате поворота на углы х₁и х_2.

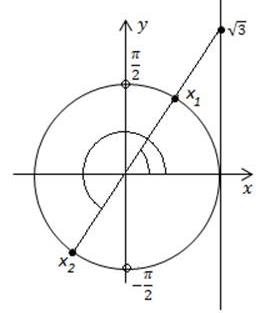
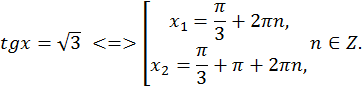
Эти два решения можно объединить и записать

Ответ: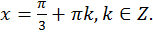

Решить уравнение: tgx = -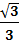

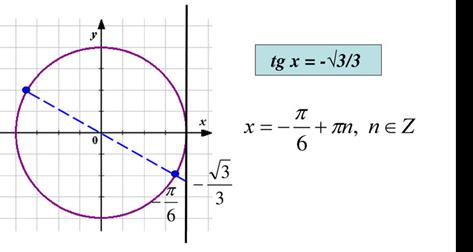
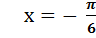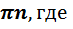
Ответ: + 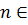Z

12 3 4 5 Следующая ⇒