
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Гиперболоиды.. Однополостный гиперболоид.. Двуполостный гиперболоид.. Параболоиды.. Эллиптический параболоид.. Гиперболический параболоид.
§4 Гиперболоиды.
4.1. Однополостный гиперболоид.
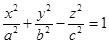 -каноническое уравнение.
-каноническое уравнение.
Метод параллельных сечений:
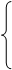 10. x=0,
10. x=0, 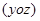
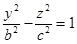 - в сечении гипербола.
- в сечении гипербола.
20. 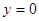 ,
, 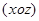
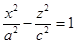 - в сечении гипербола.
- в сечении гипербола.
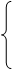 | |
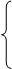 |
30. 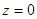 , (
, ( 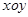 )
)
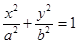 - в сечении эллипс (средний).
- в сечении эллипс (средний).
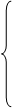 40.
40. 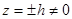 , (║
, (║ 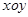 ) в сечении эллипс (верхний и нижний).
) в сечении эллипс (верхний и нижний).
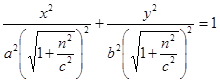
Замечание: Гиперболоиды вытянуты вдоль той оси, координаты которой в каноническом уравнении взята с минусом.
При 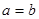
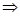
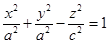 .
.
Относительный гиперболоид вращения - поверхность образованная вращением гиперболы 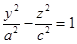 вокруг мнимой оси
вокруг мнимой оси 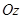 .
.
4.2. Двуполостный гиперболоид.
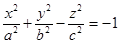 .
.
Метод параллельных сечений:
 10.
10.  ,
,
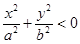 - в сечении ничего нет.
- в сечении ничего нет.
 20.
20. 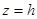 ,
, 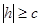 , в сечении эллипс.
, в сечении эллипс.
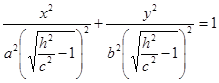 .
.
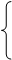
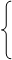 30.
30. 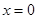 ,
, 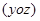
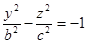
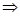
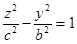 - в сечении гипербола.
- в сечении гипербола.
40.  ,
, 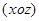
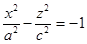
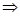
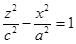
Замечание: Двуполостный гиперболоид вытянут вдоль той оси перед координатой которой стоит знак “-”.
При 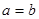
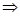
 - двуполостный параболоид вращения это поверхность получаемая врашением гиперболы
- двуполостный параболоид вращения это поверхность получаемая врашением гиперболы 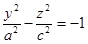 вокруг ее действительной оси
вокруг ее действительной оси  .
.
§5 Параболоиды.
5.1. Эллиптический параболоид.
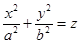 .
.
Метод параллельных сечений:
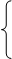
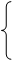 10.
10. 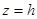 ,
, 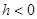
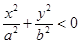 - сечения нет.
- сечения нет.
20. 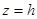 ,
, 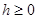
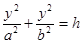 - в сечении эллипс.
- в сечении эллипс.
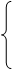 30.
30. 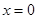 ,
, 
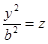 - в сечении парабола.
- в сечении парабола.
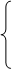 40.
40. 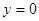
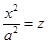 - в сечении парабола.
- в сечении парабола.
Замечание: Эллиптический параболоид вытянут вдоль той оси координата которой в первой степени.
При 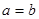 ,
,  - параболоид вращения- поверхность получаемая вращением параболы
- параболоид вращения- поверхность получаемая вращением параболы 
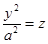 вокруг ее оси
вокруг ее оси  .
.
5.2. Гиперболический параболоид.
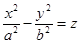 .
.
Метод параллельных сечений:
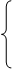 10.
10. 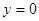 ,
, 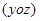
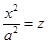 - в сечении парабола.
- в сечении парабола.
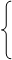 20.
20. 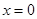
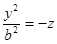 - в сечении парабола.
- в сечении парабола.
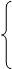
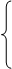
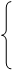 30.
30. 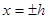 , ║
, ║ 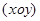
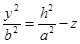 - парабола.
- парабола.
40. 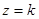 ,
, 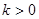 , ║
, ║ 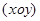
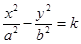 - гипербола.
- гипербола.
50. 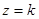 ,
, 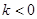 , ║
, ║ 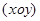

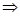
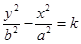 - сопряженная гипербола.
- сопряженная гипербола.
Иногда эту поверхность назвывают гиперболическим седлом. Поверхность получается если вершину параболы из 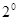 перемещать по параболе
перемещать по параболе 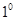 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|