
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение.. Закон больших чисел.. Для каждого положительного числа при неограниченном увеличении числа независимых повторений испытания с двумя исходами вероятность того, что частота появления «успеха» отличается менее чем на от вероятности «успеха» в
Решение.
Считаем, что опрос 1500 человек происходит независимо и что вероятность поддержки политика П. отдельным респондентом, т. е. вероятность 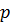 «успеха», равна 0,4. Тогда
«успеха», равна 0,4. Тогда
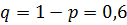 и
и 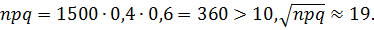
Значит, мы имеем дело с частным случаем схемы Бернулли, в которой число «успехов»  находится в пределах от 570 до 630.
находится в пределах от 570 до 630.

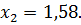
Поэтому 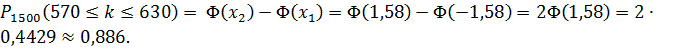
11. Анализ и сравнение изученных вероятностей.
Видим, что значение вероятности в данном случае гораздо больше по значению, чем то, которое мы определяли в предыдущей задаче.
Допустим теперь, что мы провели 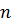 независимых повторений испытания с двумяы исходами и пусть «успех» мы наблюдали равно
независимых повторений испытания с двумяы исходами и пусть «успех» мы наблюдали равно 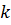 раз. Тогда число
раз. Тогда число  естественно назвать частотой «успеха». Насколько же частота «успеха» в
естественно назвать частотой «успеха». Насколько же частота «успеха» в  испытаниях Бернулли отличается от вероятности
испытаниях Бернулли отличается от вероятности 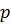 «успеха» в одном испытании? Использование функций
«успеха» в одном испытании? Использование функций 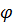 и
и 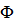 позволяет доказать, что при достаточно большом числе
позволяет доказать, что при достаточно большом числе 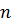 повторений испытаний с двумя исходами числа
повторений испытаний с двумя исходами числа  и
и 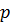 практически совпадают. Об этом говорит один их важнейших законов в теории вероятностей – закон больших чисел.
практически совпадают. Об этом говорит один их важнейших законов в теории вероятностей – закон больших чисел.
12. Закон больших чисел.
Для каждого положительного числа при неограниченном увеличении числа независимых повторений испытания с двумя исходами вероятность того, что частота появления «успеха» отличается менее чем на от вероятности «успеха» в одном отдельном испытании, стремится к единице.
В частности, если нам неизвестна вероятность случайного события А, которое может происходить или не происходить в результате некоторого испытания, то мы можем многократно повторять это испытание и вычислять частоту наступления этого события А. При большом числе повторений практически несомненно, что таким образом найденная частота приблизительно будет равна вероятности Р(А) этого случайного события.
14. Домашнее задание.
: № 25.9 (а, б); № 25.10 (б); № 25.14 (а, б); № 25.16
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|