Функция Ее геометрический смысл и график.

9. Функция Ее геометрический смысл и график.

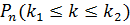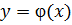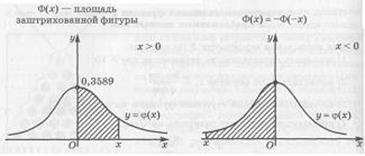
Для вычисления вероятностей снова используют гауссову функцию . Удобнее только ввести сначала некоторую дополнительную функцию Ф. Для этой функции также составлены таблицы значений, а связана она с 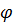следующим образом. Если аргумент х положителен, то Ф(х) равно площади под гауссовой кривой на отрезке от 0 до х. Более точно, 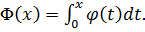Если х < 0, то Ф(х) = - Ф(х).

На интерактивную доску выводятся следующие графики.

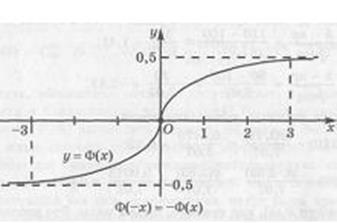
Кроме того, из графиков видно, Ф(0) = 0. Значит, функция Ф нечетна, а ее график симметричен относительно начала координат. Ясно также, что эта функция возрастает на всей прямой. График функции 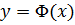изображен на рисунке ниже.

На интерактивную доску выводятся график.

10. Алгоритм использования функции в приближенных вычислениях. Задача.

Алгоритм решения задач на нахождение 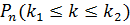аналогичен уже рассмотренному для .

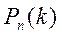Алгоритм использования функции в приближенных вычислениях

Для вычисления вероятности 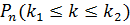следует:

1) проверить справедливость неравенства npq 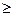10;

2) вычислить 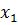и 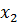по формулам

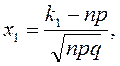
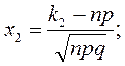
3) по таблице вычислить значения 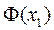и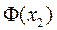

4) найти разность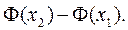

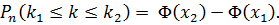
Задача.

Политика П. поддерживает в среднем 40% населения. Какова вероятность того, что из 1500 случайно опрошенных людей политика П. поддерживают от 570 до 630 человек?

⇐ Предыдущая 1 234 Следующая ⇒