
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Алгоритм использования функции Гаусса в приближенных вычислениях.
7. Алгоритм использования функции Гаусса в приближенных вычислениях.
Алгоритм использования функции в приближенных вычислениях
Для вычисления вероятности 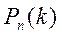 следует:
следует:
1) проверить справедливость неравенства npq 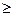 10;
10;
2) вычислить 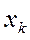 по формуле
по формуле 
3) по таблице значений гауссовой функции вычислить 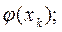
4) предыдущий результат разделить на 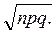
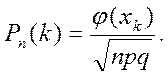
Рассмотрим внимательнее неравенство npq 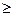 10. Так как
10. Так как 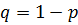 , то
, то 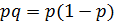 и наибольшее значение этого квадратичного выражения (относительно
и наибольшее значение этого квадратичного выражения (относительно 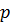 ) достигается при
) достигается при 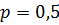 . Наибольшее значение равно 0,25. Значит,
. Наибольшее значение равно 0,25. Значит,
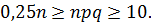
Поэтому из условия 1) алгоритма следует, что  . Это значит, что указанный алгоритм дает хорошую точность приближения, когда испытание с двумя исходами независимо повторяется как минимум несколько десятков раз. При меньшем числе повторений точность приближения резко ухудшается.
. Это значит, что указанный алгоритм дает хорошую точность приближения, когда испытание с двумя исходами независимо повторяется как минимум несколько десятков раз. При меньшем числе повторений точность приближения резко ухудшается.
Задача.
Вероятность рождения мальчика примем равной 50%. Найти вероятность того, что среди 200 новорожденных будет 110 мальчиков.
Решение:
Будем действовать по предложенному алгоритму. В нашем случае п = 200, p = q = 0,5. Значит, npq = 50 > 10 и 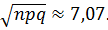 При этом число «успехов»
При этом число «успехов» 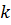 равно 110.
равно 110.
Тогда:
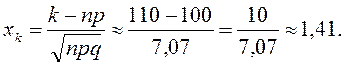
Используя таблицы, вычисляем ответ:
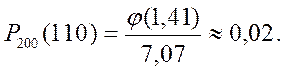
8. Вероятность 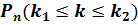 того, что число «успехов»
того, что число «успехов» 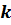 в
в 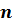 испытаниях Бернулли находится в пределах от
испытаниях Бернулли находится в пределах от 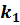 до
до 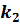 .
.
Вероятности 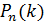 , как правило, весьма малы. Это вполне объяснимо даже и без вычислений, на интуитивном уровне. Если монету бросить 1000 раз, то практически невероятно выпадение ровно 694 «орлов» или именно 427 «решек» и т. п. Поэтому при большом числе п в схеме Бернулли для числа k «успехов» устанавливают не одно точное значение, а некоторые рамки, в пределах которых разрешено меняться числу
, как правило, весьма малы. Это вполне объяснимо даже и без вычислений, на интуитивном уровне. Если монету бросить 1000 раз, то практически невероятно выпадение ровно 694 «орлов» или именно 427 «решек» и т. п. Поэтому при большом числе п в схеме Бернулли для числа k «успехов» устанавливают не одно точное значение, а некоторые рамки, в пределах которых разрешено меняться числу 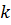 .Например, найти вероятность того, что в 1000 бросаниях монеты «орел» выпадет от 500 до 600 раз, или вероятность того, что среди 200 новорожденных будет от 70 до 110 мальчиков. Вероятность того, что число «успехов»
.Например, найти вероятность того, что в 1000 бросаниях монеты «орел» выпадет от 500 до 600 раз, или вероятность того, что среди 200 новорожденных будет от 70 до 110 мальчиков. Вероятность того, что число «успехов» 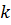 в
в 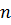 испытаниях Бернулли находится в пределах от
испытаниях Бернулли находится в пределах от 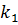 до
до 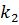 , обозначают так:
, обозначают так: 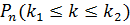 .
.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|