
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Пример 2. Решение единственное. Пример 3. Пример 4. Найти опорное решение. Выводы
Пример 2
х1 + 4х2 - х4 = 5
2х1 - 3х2 + х3 + х4 = 3
х1 + 2х3 - х4 = 3
2х2 - 3х3 + 2х4 = 3
4-шага модифицированных жордановых исключений.
| - х1 | -х2 | -х3 | - х4 | ||
| - 1 | |||||
| -3 | |||||
| - 1 | |||||
| -3 |
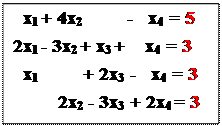
| -х2 | -х3 | - х4 | ||
| -2 | ||||
| -3 | -3 | -3 | ||
| х1 | - 1 | |||
| -3 |
| -х3 | ||
| -3 | -1 | |
| х2 | 5/4 | -1/4 |
| х1 | 3/4 | 13/4 |
| х4 | 1/4 | -5/4 |
| х3 | |
| х2 | |
| х1 | |
| х4 |
| -х3 | - х4 | ||
| -2 | -6 | ||
| х2 | -1 | ||
| х1 | - 1 | ||
| -5 |
Решение единственное
Пример 3
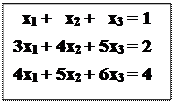
| -х1 | -х2 | -х3 | ||
| -х2 | -х3 | ||
| х1 | |||
| -1 | |||
| -х3 | ||
| х1 | -1 | |
| -1 | ||
| х2 |
Система несовместна т.к. во 2-й строке свободный член равен (-1), а все остальные элементы нули.
Пример 4. Найти опорное решение
|
1. Т.к. в исходной таблице все свободные члены должны быть неотрицательны, то третье уравнение умножим на (-1).
2. В качестве разрешающего элемента можно взять любой столбец, содержащий хотя бы один положительный элемент.
| - х1 | -х2 | -х3 | - х4 | ||
| 3 | 2 | -1 | - 1 | ||
| 2 | 2 | -1 | |||
| 1 | -3 |
| - х1 | -х2 | - х4 | ||
| 2 | 5 | -1 | - 2 | |
| 2 | 2 | -1 | ||
| х3 | 1 | -3 |
Разрешающую строку в первой таблице определим по наименьшему отношению свободных членов к положительным элементам третьего столбца (минимальное симплексное отношение).
min (3/1, 1/1).
Во - второй таблице разрешающим выбран первый столбец, а строка из отношений
min( 2/5, 2/2)
| - х2 | - х4 | ||
| х1 | 2/5 | -1/5 | - 2/5 |
| 6/5 | -3/5 | 9/5 | |
| х3 | 11/5 | -3/5 | -1/5 |
| - х2 | ||
| х1 | 2/3 | -1/5 |
| х4 | 2/3 | -3/5 |
| х3 | 7/3 | -3/5 |
При х2 =0 опорное решение (2/3, 0, 7/3, 2/3)
Выводы
Поскольку число переменных n в системе больше числа уравнений m то, одно из возможных решений можно найти, если (n – m) переменных положить равными нулю. Полученная система из m уравнений и m неизвестных должна иметь определитель, составленный из коэффициентов при неизвестных, не равный нулю. Если это условие не выполняется, то нулю приравниваются другие переменные.
Базисомназывается любой набор m переменных таких, что определитель, составленный из коэффициентов, при этих переменных не равен нулю. Эти m переменных называются базисные переменные. Базисные переменные – независимые переменные. Остальные – не базисные или свободные.
Т.о., если положить все свободные переменные равными нулю и решить систему из m уравнений и m неизвестных, то получим базисное решение.
Неотрицательные базисные решения называется опорными планами.
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|