
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Решение систем линейных уравнений с помощью жордановых исключений
Решение систем линейных уравнений с помощью жордановых исключений
Модифицированные жордановы исключения
Часто пользуются модифицированными жордановыми исключениями. В этом случае жордановы таблицы отличаются тем, что в них
v переменные в заглавной строке записываются со знаком минус (независимые переменные),
v i-й шаг жорданова исключения переводит эту исходную таблицу в любую по правилу:
- разрешающий элемент заменяется обратной величиной
- остальные элементы разрешающей строки делятся на разрешающий элемент
- остальные элемента разрешающего столбца делятся на разрешающий элемент и меняют знаки
- прочие элементы вычисляются по формуле
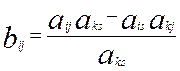
После каждого шага жордановых исключений вычеркивается разрешающий столбец и строки, содержащие целиком нулевые элементы.
Пример 1. Решить систему, пользуясь модифицированными жордановыми исключениями. Не забывать пересчитать свободные члены.
|
Решение
1. Запишем СЛАУ в форме жордановой таблицы
| - х1 | -х2 | -х3 | - х4 | ||
| -3 | - 6 | ||||
| - 4 | |||||
| - 2 |
2. Проделать возможное число модифицированных жордановых исключений
ü Ввести в базис, например, - х2
| - х1 |  -х2 -х2
| -х3 | - х4 | ||
| -3 | - 6 | ||||
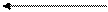 0 0
| 0 | - 4 | |||
| 3 | - 2 |
| -х1 | -х3 | - х4 | |||
| х2 | |||||
|

ü Используя данные исходной таблицы пересчитать элементы разрешающей строки и разрешающего столбца, по правилу:
- разрешающий элемент заменить обратной величиной
- остальные элементы разрешающей строки разделить на разрешающий элемент
- остальные элементы разрешающего столбца разделить на разрешающий элемент и поменять знаки
ü пересчитать остальные элементы таблицы по правилу
| -х1 | -х3 | - х4 | |||
| bij | -2 | ||||
| х2 | - 4 | ||||
 | |||
 | |||

|
|
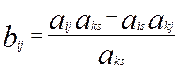
| -х1 | -х3 | - х4 | |||
| -3 |   1 1
| - 6 | |||
| х2 | 0 | - 4 | |||
| 3 | - 2 |
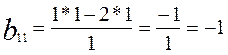
| -х1 | -х3 | - х4 | |||
| -1 | -2 | ||||
| х2 | 0 | - 4 | |||
| -х1 | -х3 | - х4 | |||
| -3 |   2 2
| - 6 | |||
| х2 | 0 | - 4 | |||
| 3 | - 2 |
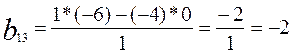
| -х1 | -х3 | - х4 | |||
| -1 | -2 | -2 | |||
| х2 | 0 | - 4 | |||
В результате получим следующую таблицу
| -х1 | -х3 | - х4 | |||
| -3 | -1 | -2 | -1 | ||
| х2 | 0 | - 4 | |||
| 3 | - 2 |
ü Из нее вычеркиваем столбец с 0 в заглавной строке
 -х1 -х1
| -х3 | - х4 | ||
| -3 | -1 | -1 | ||
| х2 | 0 | - 4 | ||
 0 0
| 3 | - 2 |
ü В этой таблице введем в базис х1
| -х3 | - х4 | |||
| -3 | -1 | -1 | ||
| х2 | 0 | - 4 | ||
| х1 | 3 | - 2 |
ü Пересчитаем опять всю таблицу
| -х3 | - х4 | ||
| х2 | -3 | - 2 | |
| х1 | - 2 |
| -х3 | - х4 | |||
| х2 | -3 | -1 | - 2 | |
| х1 | 3 | - 2 |
ü Получили решение:
х1= - х3 + 2х4 + 3 х1, х2 -базисные переменные
х3 и х4 могут принимать любые значения свободные переменные
 |

| ||||
| ||||
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|