Жордановы исключения. Шаг жорданова исключения

Жордановы исключения

При переходе от одного базисного решения к другому нам необходимо выражать одни переменные через другие. Т.е. зависимые делать независимыми и наоборот.

Рассмотрим пример:

Дана система:

y₁= 2х₁- 5х₂+ 4х₃ (1)

y₂= 8х₁+ 2х₂- 3х₃(2)

- решим уравнение (2) относительно х₃

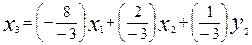
-подставим решение в (1)

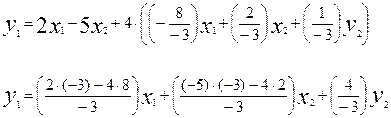Получим систему уравнений:

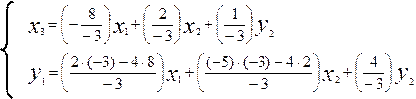Перепишем (1) и (2) и эту систему в виде таблиц:

	х₁	x₂	y₂
y₁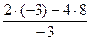
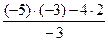
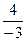
х₃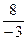

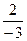
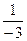
y₁= 2х₁- 5х₂+ 4х₃

y₂= 8х₁+ 2х₂- 3х₃

	х₁	x₂	х₃
y₁	2	- 5
y₂			- 3

Обратите внимание, коэффициенты, стоящие в ячейках второй таблицы вычисляются по правилу диагоналей.

«Элемент b_ij равен разности произведения элементов, расположенных на главной диагонали и побочной диагонали, деленной на разрешающий элемент».

Элемент -3 называется разрешающим, т.е. это элемент, который находится на пересечении строки и столбца, с которыми произведен шаг жорданова исключения.

Операция, произведенная над таблицей 1 с разрешающим элементом называется –

Шаг жорданова исключения

Ø разрешающий элемент заменяется обратной величиной

Ø остальные элементы разрешающей строки делятся на разрешающий элемент и меняют знаки

Ø остальные элементы разрешающего столбца делят на разрешающий элемент,

Ø прочие вычисляются по формуле (или по правилу диагоналей)


b_ij	a_is
a_kj	a_is	- 4

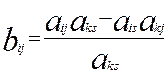
Главная диагональ соединяет преобразуемый и разрешающий элементы. Другая диагональ – побочная.

12 3 4 Следующая ⇒