Шаровый сегмент. Шаровый сектор

Рис. 4.

Радиус шара –любой отрезок, соединяющий центр и какую-нибудь точку сферы.

Диаметр шара –отрезок, соединяющий две точки сферы и проходящий через ее центр. Диаметр сферы равен 2R.

Центр шара – точка О.

Теорема: Объем шара радиуса R равен

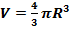где 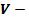объём шара;

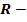радиус шара;

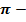постоянная, равная 3, 14.

Части шара

Шаровый сегмент

часть шара отсекаемая от него какой-нибудь плоскостью

Шаровый сектор

тело, полученное вращением кругового сектора с углом, меньшим , вокруг прямой, содержащей один из ограничивающих круговой сектор радиусов

Шаровый слой часть шара, заключенная между двумя параллельными секущими плоскостями

Объем шарового сегмента:

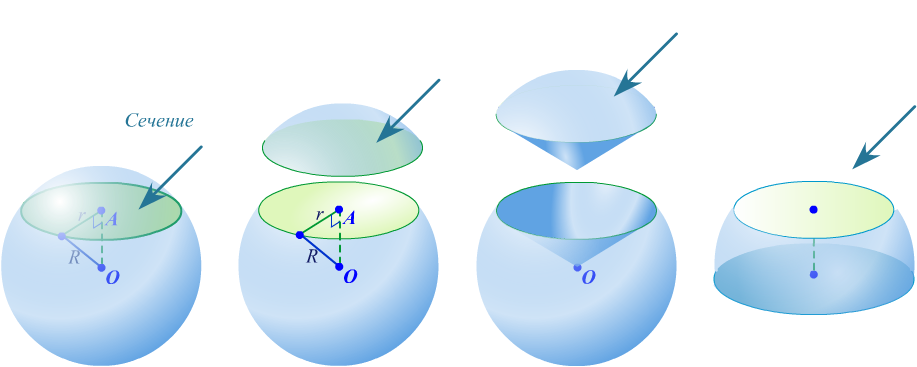
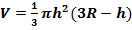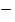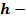, где V объем шарового сегмента; радиус шара; высота сегмента 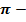постоянная, равная 3, 14.

Объем шарового сектора:

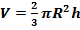где V 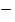объем щарового сектора;

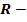радиус шара;

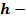высота сектора

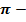постоянная, равная 3, 14.

Объем шарового слоя:

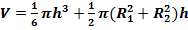где 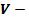объем шарового слоя;

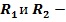радиусы оснований слоя;

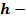высота слоя

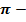постоянная, равная 3, 14.

Площадь сегментовой поверхности:

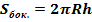, где 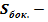площадь сегментовой поверхности шара; 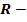радиус шара; 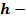высота сегмента 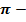постоянная, равная 3, 14.

Площадь полной поверхности:

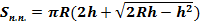где 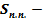площадь полной поверхности шарового сектора;

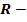радиус шара;

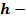высота сегмента

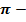постоянная, равная 3, 14.

Площадь боковой поверхности:

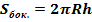где 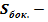площадь боковой поверхности шарового слоя;

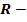радиус шара;

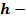высота сегмента

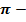постоянная, равная 3, 14.

2.Образец выполнения упражнений:

1. Напишите уравнение сферы радиуса R с центром А, если: