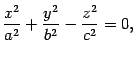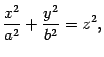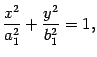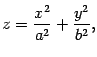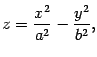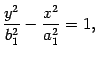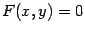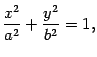- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Конус. Параболоиды
Конус
Определение 13.6 Конусом второго порядка называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
| (13.10) |
где 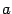 ,
, 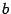 ,
, 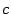 -- положительные числа.
-- положительные числа.
Замечание 13.1 С математической точки зрения поверхность (13.10) лучше определять с помощью уравнения
|
| (13.11) |
так как в нем меньше параметров, но при этом, во-первых, теряется аналогия с уравнениями предыдущих поверхностей, а во-вторых, если считать, что величины 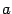 ,
, 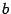 ,
, 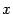 ,
,  ,
, 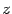 имеют размерность длины, то в уравнении (13.11) размерности правой и левой части не согласуются.
имеют размерность длины, то в уравнении (13.11) размерности правой и левой части не согласуются.
Для краткости в дальнейшем конус второго порядка будем называть просто конус. Исследуем форму конуса. Так же, как эллипсоид и гиперболоиды, он имеет три плоскости симметрии, три оси симметрии и центр симметрии. Ими являются соответственно координатные плоскости, координатные оси и начало координат.
Для построения конуса найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 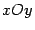 . На этой плоскости
. На этой плоскости 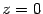 , поэтому
, поэтому
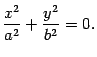
Координаты только одной точки плоскости 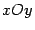 могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью
могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью 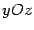 . На этой плоскости
. На этой плоскости 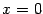 , поэтому
, поэтому
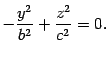
Это уравнение пары прямых 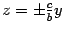 на плоскости
на плоскости 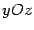 . Построим эти прямые (рис. 13.16). Сечение плоскостью
. Построим эти прямые (рис. 13.16). Сечение плоскостью 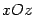 также является парой прямых с уравнением
также является парой прямых с уравнением 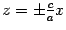 . Нарисуем и эти прямые (рис. 13.16).
. Нарисуем и эти прямые (рис. 13.16).
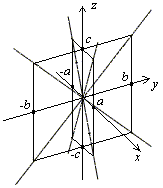
Рис.13.16.Сечения конуса координатными плоскостями
Найдем линии пересечения поверхности с плоскостями 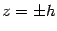 ,
, 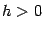 . Уравнения этих линий
. Уравнения этих линий
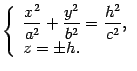
Первое уравнение преобразуем к виду
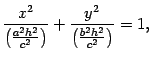
то есть к виду
|
| (13.12) |
где 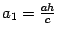 ,
, 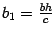 . Уравнение (13.12) является уравнением эллипса. Нарисуем полученные сечения (рис. 13.17).
. Уравнение (13.12) является уравнением эллипса. Нарисуем полученные сечения (рис. 13.17).
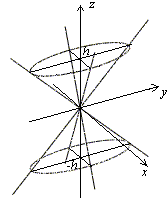
Рис.13.17.Изображение конуса с помощью сечений
Привычное для глаза изображение приведено на рисунке 13.18.
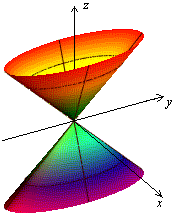
Рис.13.18.Конус
Точка пересечения конуса с плоскостью 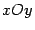 называется вершиной конуса.
называется вершиной конуса.
Если в уравнении (13.10) 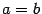 , то сечения конуса плоскостями параллельными плоскости
, то сечения конуса плоскостями параллельными плоскости 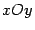 являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости
являются окружностями. В этом случае поверхность называется прямым круговым конусом и может быть получена вращением прямой, лежащей в плоскости 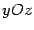 , вокруг оси
, вокруг оси 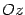 . Именно с таким конусом мы имеем дело в школьном курсе математики.
. Именно с таким конусом мы имеем дело в школьном курсе математики.
Параболоиды
Определение 13.7 Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
| (13.13) |
где 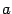 и
и 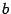 -- положительные числа.
-- положительные числа.
Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости 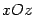 ,
, 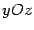 и координатная ось
и координатная ось 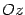 .
.
Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 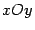 . На этой плоскости
. На этой плоскости 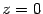 , поэтому
, поэтому
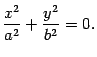
Координаты только одной точки плоскости 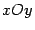 могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью
могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью 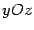 . На этой плоскости
. На этой плоскости 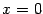 , поэтому
, поэтому

Это уравнение параболы на плоскости 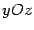 . Построим ее (рис. 13.19). Сечение плоскостью
. Построим ее (рис. 13.19). Сечение плоскостью 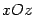 также является параболой. Нарисуем и ее (рис. 13.19). Найдем линии пересечения поверхности с плоскостью
также является параболой. Нарисуем и ее (рис. 13.19). Найдем линии пересечения поверхности с плоскостью 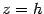 . Уравнения этой линии
. Уравнения этой линии
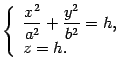
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если 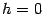 . Эта точка называется вершиной параболоида.
. Эта точка называется вершиной параболоида.
Пусть 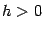 . Первое уравнение преобразуем к виду
. Первое уравнение преобразуем к виду
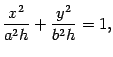
то есть к виду
|
| (13.14) |
где 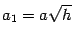 ,
,  . Уравнение (13.14) является уравнением эллипса. Нарисуем полученное сечение (рис. 13.19). При
. Уравнение (13.14) является уравнением эллипса. Нарисуем полученное сечение (рис. 13.19). При 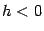 плоскость поверхность не пересекает.
плоскость поверхность не пересекает.
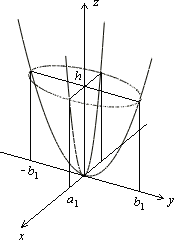
Рис.13.19.Сечения эллиптического параболоида координатными плоскостями
Найдем сечения параболоида плоскостями 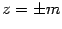 , параллельными плоскости
, параллельными плоскости 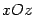 . Линии этих сечений удовлетворяют уравнениям
. Линии этих сечений удовлетворяют уравнениям
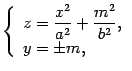
и являются параболами, такими же, как в плоскости 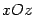 , только сдвинутыми вверх на величину
, только сдвинутыми вверх на величину 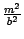 , их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью
, их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью 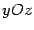 (рис. 13.20).
(рис. 13.20).
Рис.13.20.Дополнительные сечения параболоида
Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости  . Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости
. Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости  , а вершина скользила по параболе в плоскости
, а вершина скользила по параболе в плоскости 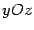 .
.
Привычное для глаза изображение приведено на рисунке 13.21.
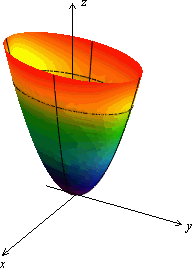
Рис.13.21.Эллиптический параболоид
Если в уравнении (13.13) 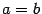 , то сечения плоскостями, параллельными плоскости
, то сечения плоскостями, параллельными плоскости 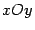 , являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости
, являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости 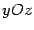 , вокруг оси
, вокруг оси 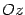 (рис. 13.22).
(рис. 13.22).

Рис.13.22.Параболоид вращения
Определение 13.8 Гиперболическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид
|
| (13.15) |
где 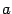 и
и 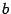 -- положительные числа.
-- положительные числа.
Исследуем форму гиперболического параболоида. Так же, как и эллиптический параболоид, он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости 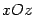 ,
, 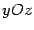 и координатная ось
и координатная ось 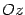 .
.
Для построения гиперболического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 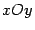 . На этой плоскости
. На этой плоскости 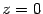 , поэтому
, поэтому
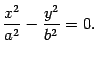
Это уравнение определяет на плоскости 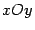 пару прямых
пару прямых 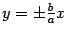 , изображенных на рисунке 13.23.
, изображенных на рисунке 13.23.
Найдем линию пересечения с плоскостью 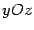 . На этой плоскости
. На этой плоскости 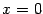 , поэтому
, поэтому
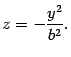
Это уравнение на плоскости 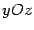 задает параболу, ветви которой направлены вниз. Построим ее (рис. 13.23). Сечение плоскостью
задает параболу, ветви которой направлены вниз. Построим ее (рис. 13.23). Сечение плоскостью 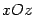 также является параболой
также является параболой
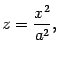
но ее ветви направлены вверх. Нарисуем и ее (рис. 13.23).
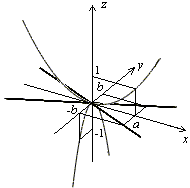
Рис.13.23.Сечения гиперболического параболоида координатными плоскостями
Найдем линии пересечения поверхности с плоскостью 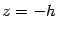 ,
, 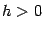 . Уравнения этой линии
. Уравнения этой линии
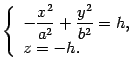
Первое уравнение преобразуем к виду
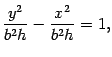
то есть к виду
|
| (13.16) |
где 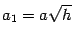 ,
,  . Уравнение (13.16) является уравнением гиперболы. Ее действительная ось параллельна оси
. Уравнение (13.16) является уравнением гиперболы. Ее действительная ось параллельна оси 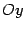 , а мнимая -- оси
, а мнимая -- оси 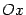 . Полуоси равны соответственно
. Полуоси равны соответственно 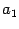 и
и 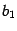 . Нарисуем полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 13.24).
. Нарисуем полученное сечение, но чтобы не перегружать рисунок линиями, асимптоты изображать не будем (рис. 13.24).
Найдем линии пересечения с плоскостями 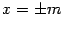 , параллельными плоскости
, параллельными плоскости 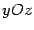 . Уравнения этих линий
. Уравнения этих линий
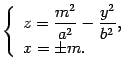
Первое из этих уравнений является уравнением параболы, такой же, как и в сечении плоскостью 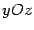 , только сдвинутой вдоль оси
, только сдвинутой вдоль оси 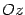 на величину
на величину 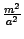 вверх. Эти параболы изображены на рисунке 13.24.
вверх. Эти параболы изображены на рисунке 13.24.
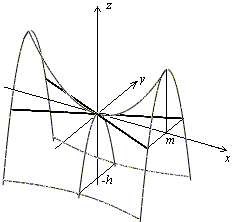
Рис.13.24.Изображение гиперболического параболоида с помощью сечений
Так как 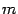 -- произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости
-- произвольное число, то вся поверхность может быть получена движением параболы, лежащей в плоскости 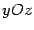 . Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости
. Передвигать параболу нужно так, чтобы ее плоскость оставалась параллельной плоскости 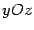 , а вершина скользила по параболе в плоскости
, а вершина скользила по параболе в плоскости 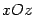 .
.
Плоскость 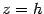 ,
, 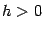 , пересекает поверхность по гиперболе, но в отличие от гиперболы (13.16), ее действительная ось параллельна теперь оси
, пересекает поверхность по гиперболе, но в отличие от гиперболы (13.16), ее действительная ось параллельна теперь оси 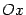 , а мнимая -- оси
, а мнимая -- оси 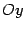 (рис. 13.25).
(рис. 13.25).
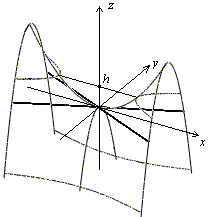
Рис.13.25.Дополнительное сечение
Привычное для глаза изображение приведено на рисунке 13.26.
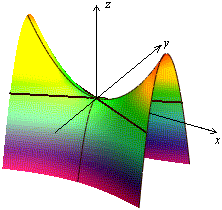
Рис.13.26.Гиперболический параболоид
Цилиндры
Определение 13.9 Цилиндрической поверхностью называется геометрическое место параллельных прямых, пересекающих данную линию. Эта линия называется направляющей, а параллельные прямые -- образующими.
Рассмотрим уравнение вида
|
| (13.17) |
и покажем, что оно определяет цилиндрическую поверхность с образующими, параллельными оси 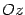 . Пусть
. Пусть 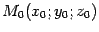 -- некоторая точка, координаты которой удовлетворяют уравнению (13.17). Поскольку в это уравнение не входит явно переменная
-- некоторая точка, координаты которой удовлетворяют уравнению (13.17). Поскольку в это уравнение не входит явно переменная 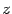 , ему будут удовлетворять координаты всех точек
, ему будут удовлетворять координаты всех точек 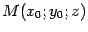 , где
, где 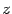 -- любое число. Следовательно, при любом
-- любое число. Следовательно, при любом 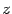 точка
точка 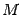 лежит на поверхности, определяемой уравнением (13.17). Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку
лежит на поверхности, определяемой уравнением (13.17). Отсюда следует, что на поверхности целиком лежит прямая, проходящая через точку 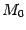 параллельно оси
параллельно оси 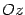 . А это означает, что поверхность, определяемая уравнением (13.17), составлена из прямых, параллельных оси
. А это означает, что поверхность, определяемая уравнением (13.17), составлена из прямых, параллельных оси 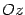 , то есть она является цилиндрической поверхностью.
, то есть она является цилиндрической поверхностью.
Заметим, что на плоскости 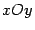 уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.
уравнение (13.17) определяет направляющую рассматриваемой цилиндрической поверхности.
Итак, делаем вывод, что если уравнение поверхности не содержит в явном виде какой-либо переменной, то это уравнение определяет в пространстве цилиндрическую поверхность с образующими, параллельными оси отсутствующего переменного и направляющей, которая в плоскости двух других переменных имеет то же самое уравнение.
Нас будут интересовать только те цилиндрические поверхности, которые являются поверхностями второго порядка, а это значит, что уравнение (13.17), их задающее будет иметь вид (13.1).
Определение 13.10 Поверхность, которая в некоторой декартовой системе координат задается уравнением
|
| (13.18) |
называется эллиптическим цилиндром, поверхность, которая задается уравнением
|
| (13.19) |
называется гиперболическим цилиндром, а которая задается уравнением
|
| (13.20) |
называется параболическим цилиндром.
Для того чтобы построить поверхность, задаваемую уравнением (13.18), или уравнением (13.19), или (13.20), достаточно нарисовать на плоскости 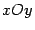 направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси
направляющую, уравнение которой на этой плоскости совпадает с уравнением самой поверхности, и затем через точки направляющей провести образующие параллельно оси 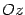 . Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости
. Для наглядности следует построить также одно-два сечения плоскостями, параллельными плоскости 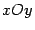 . В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.
. В каждом таком сечении получим такую же кривую, как и исходная направляющая. Изображения этих цилиндров сечениями приведены на рисунках 13.27, 13.29 и 13.31, а их объемные изображения -- на рисунках 13.28, 13.30 и 13.32.
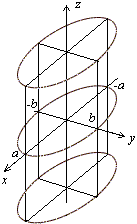
Рис.13.27.Изображение эллиптического цилиндра с помощью сечений
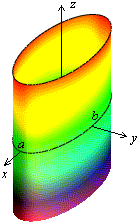
Рис.13.28.Эллиптический цилиндр
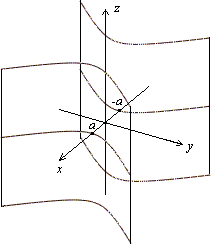
Рис.13.29.Изображение гипербоического цилиндра с помощью сечений
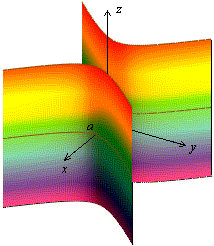
Рис.13.30.Гиперболический цилиндр
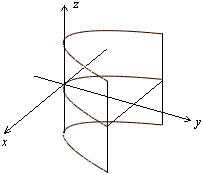
Рис.13.31.Изображение параболического цилиндра с помощью сечений
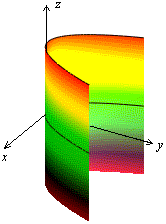
Рис.13.32.Параболический цилиндр
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|