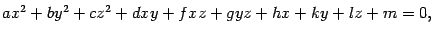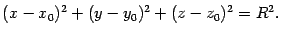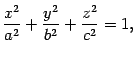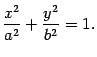Поверхности второго порядка

Поверхности второго порядка

Определение 13.1 Поверхностью второго порядка называется поверхность, определяемая уравнением

(13.1)

где 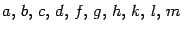-- вещественные числа, причем хотя бы одно из чисел

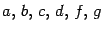отлично от нуля.

В дальнейшем будет показано, что поверхности второго порядка, за исключением случаев сильного вырождения, можно разделить на пять классов: эллипсоиды, гиперболоиды, параболоиды, конусы и цилиндры. Для каждой из поверхностей существует декартова прямоугольная система координат, в которой поверхность задается простым уравнением, называемым каноническим уравнением. Этот факт будет обоснован позже.

Сфера

Определение 13.2 Сферой называется геометрическое место точек пространства, равноудаленных от фиксированной точки, называемой центром.

Теорема 13.1 Сфера радиуса 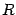с центром в точке 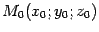имеет уравнение

(13.2)

Доказательство аналогично доказательству теоремы 3.1.

Пример 13.1 Нарисуйте сферу

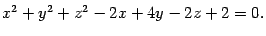
Решение. Выделив полные квадраты, получим

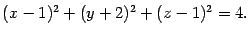
Значит, центром сферы является точка 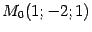, радиус сферы равен 2.

Для ее изображения нарисуем сечения сферы плоскостями, проходящими через центр и параллельными координатным плоскостям. Каждое такое сечение будет окружностью радиуса 2 с центром в точке 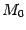(рис 4.1).

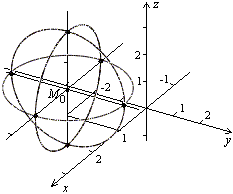
Рис.13.1.Сфера, изображенная сечениями

Более "художественное" изображение сферы приведено на рисунке 13.2

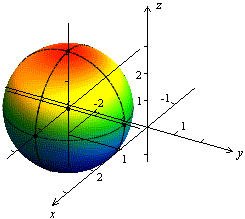
Рис.13.2.Сфера

Определение 13.3 Эллипсоидом называется поверхность, каноническое уравнение которой имеет вид

(13.3)

где 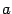, , 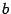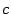-- положительные числа.

Исследуем форму эллипсоида. Из уравнения (13.3) видно, что координаты точек поверхности ограничены: , , .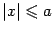

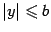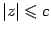Эллипсоид обладает тремя плоскостями симметрии, тремя осями симметрии и центром симметрии. Ими служат соответственно координатные плоскости, координатные оси и начало координат..

Для выяснения формы эллипсоида рассмотрим его сечения плоскостями. Найдем линию пересечения эллипсоида с плоскостью 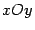. Так как любая точка плоскости 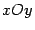имеет нулевую третью координату, 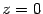, то координаты точек эллипсоида на плоскости 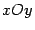удовлетворяют уравнению

(13.4)

получаем, что линия пересечения является эллипсом с полуосям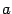и и 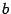(рис. 13.3).

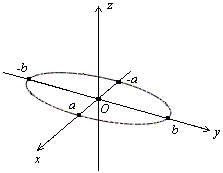
Рис.13.3.Сечение плоскостью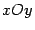

Аналогично, сечение в плоскости 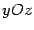дает эллипс

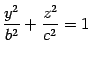
с полуосям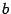и и 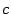, а сечение плоскостью 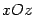-- эллипс

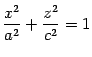
с полуосям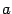и и 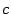(рис. 13.4)

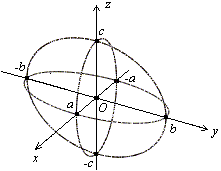
Рис.13.4.Сечения эллипсоида координатными плоскостями

Нарисованный "каркас" из сечений уже дает представление об эллипсоиде. Но чтобы выяснить, как ведет себя поверхность между нарисованными кривыми, рассмотрим сечение эллипсоида плоскостью 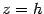. Эта плоскость параллельна плоскости 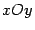и пересекает ось 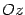в точке 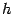. Уравнения этой линии

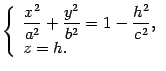
Очевидно, что если 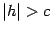, то ни одна точка пространства не может удовлетворять этой системе: в левой части первого уравнения стоит неотрицательное число, а в правой -- отрицательное.

Если 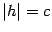, то сечении получим лишь одну точку 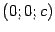или 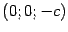в зависимости от знака .

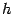Пусть 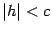. Тогда первое уравнение преобразуем к виду

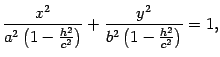
то есть к виду

(13.5)

где 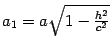, 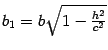. Уравнение (13.5) является уравнением эллипса, подобного эллипсу, задаваемому уравнением (13.4), с коэффициентом подобия 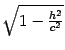и полуосям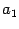и и 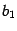. Ясно, что сечение плоскостью 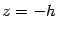является таким же эллипсом, расположенным симметрично первому относительно плоскости 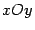. Нарисуем эти сечения (рис. 13.5).

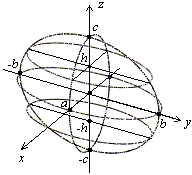
Рис.13.5.Дополнительные сечения эллипсоида

Таким образом, весь эллипсоид составлен из эллипсов, лежащих в плоскостях, параллельных плоскости 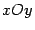и подобных эллипсу в плоскости 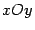. Рисунок 13.6 дает более привычное глазу изображение эллипсоида.

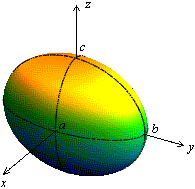
Рис.13.6.Эллипсоид

Так же, как для эллипса, точки пересечения эллипсоида с координатными осями называются вершинами эллипсоида, центр симметрии -- центром эллипсоида. Числа 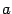, , 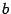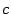называются полуосями. Если полуоси попарно различны, то эллипсоид называется трехосным.

Если две полуоси равны друг другу, то эллипсоид называется эллипсоидом вращения. Эллипсоид вращения может быть получен вращением эллипса вокруг одной из осей. Например, если 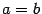, то все сечения эллипсоида плоскостями 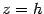, , 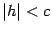будут окружностями. Сам эллипсоид может быть получен из эллипса

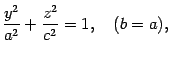
лежащего в плоскости 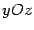, при вращении его вокруг оси 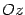(рис. 13.7).

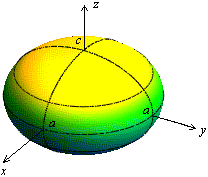
Рис.13.7.Эллипсоид вращения

12 3 4 Следующая ⇒