Параболоиды. Определение

Параболоиды

Определение

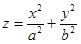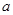Эллиптическим параболоидом называется поверхность, уравнение которой в некоторой декартовой системе координат имеет вид , где и 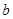- положительные числа.

Исследуем форму эллиптического параболоида. Он имеет две плоскости симметрии и ось симметрии. Ими являются соответственно координатные плоскости 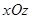, 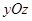и координатная ось .

Для построения эллиптического параболоида найдем его сечения различными плоскостями. Найдем линию пересечения с плоскостью 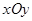. На этой плоскости 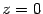, поэтому .

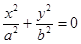Координаты только одной точки плоскости 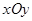могут удовлетворять данному уравнению, а именно, начала координат. Найдем линию пересечения с плоскостью 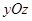. На этой плоскости 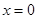, поэтому .

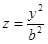Это уравнение параболы на плоскости 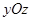. Построим ее (рис. 19). Сечение плоскостью 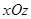также является параболой. Найдем линии пересечения поверхности с плоскостью 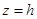. Уравнения этой линии

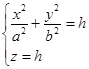
Очевидно, что только одна точка (начало координат) удовлетворяет этим уравнениям, если 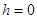. Эта точка называется вершиной параболоида.

Пусть 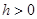. Первое уравнение преобразуем к виду , то есть к виду 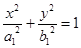, где , . Полученное уравнение является уравнением эллипса. Изобразим полученное сечение (рис.19). При 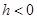плоскость поверхность не пересекает.

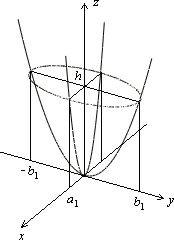
Рис.19.Сечения эллиптического параболоида координатными плоскостями

Найдем сечения параболоида плоскостями 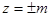, параллельными плоскости 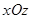. Линии этих сечений удовлетворяют уравнениям 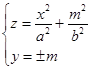и являются параболами, такими же, как в плоскости 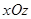, только сдвинутыми вверх на величину 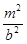, их вершины при таком сдвиге лежат на параболе, получившейся в сечении плоскостью 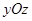(рис. 20).

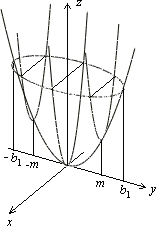
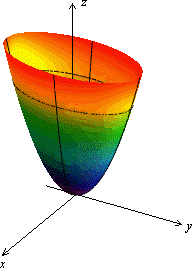
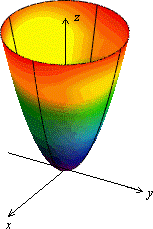
Рис.20 Дополнительное сечение Рис. 21.Эллиптический параболоид Рис. 22.Параболоид вращения

Следовательно, вся поверхность может быть получена движением параболы, лежащей в плоскости 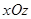. Парабола должна двигаться так, чтобы ее плоскость была параллельна плоскости 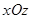, а вершина скользила по параболе в плоскости .

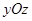Если в уравнении 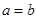, то сечения плоскостями, параллельными плоскости 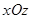, являются окружностями. В этом случае поверхность называется параболоидом вращения и может быть образована вращением параболы, лежащей в плоскости 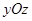, вокруг оси 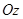(рис. 22).

⇐ Предыдущая 1 2 3 4 567 8 9 10 Следующая ⇒