Контакты

Случайная статья

Поверхность вращения. Эллипсоид. Гиперболоиды. Параболоиды. Эллиптический параболоид

⇐ ПредыдущаяСтр 3 из 4Следующая ⇒

Поверхность вращения

Пусть линия 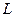, лежащая в плоскости 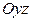, задана уравнениями:

.

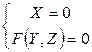Рассмотрим поверхность, образованную вращением этой линии относительно оси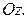

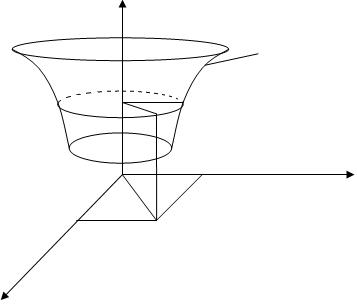
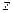
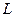
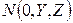
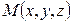
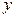
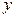
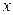
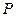
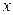
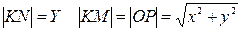
Так как точки линии 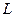описывают окружности, то

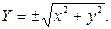
Уравнение поверхности вращения

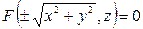
получается заменой координат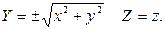

Пример: Найти уравнение поверхности вращения эллипса.

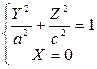относительно оси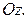

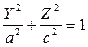замена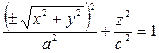

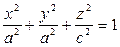- эллипсоид вращения.

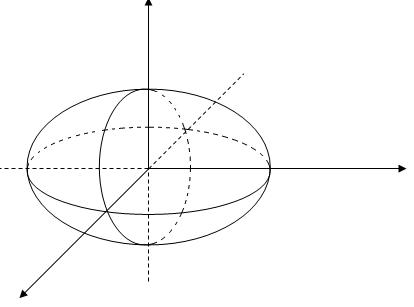
Эллипсоид

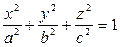- эллипсоид, 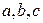- полуоси эллипса

Эллипсоид симметричен относительно координатных плоскостей. Пересечём его плоскостями, параллельными координатным плоскостям.

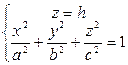
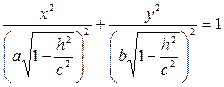
- это эллипс. При возрастании 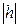- полуоси уменьшаются, при 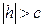пересечения нет. При пересечении 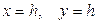тоже получаются эллипсы.

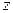
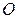
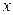
Гиперболоиды

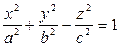
- однополостный гиперболоид.

Три координатные плоскости – три плоскости симметрии.

Сечения:

1. 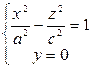- гипербола

2. 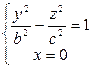- гипербола

3.

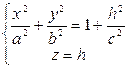
- эллипс

При 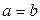, 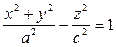- однополосный гиперболоид вращения.

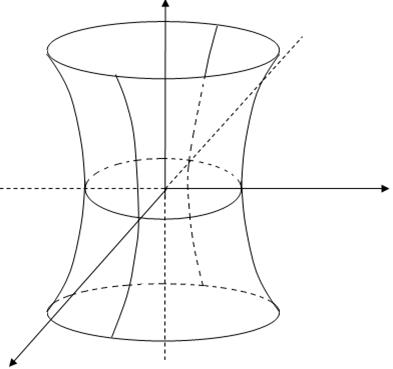
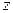
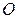
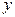
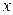
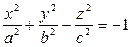
- двуполосный гиперболоид.

Пересекаем плоскостям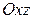и и 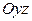, получим

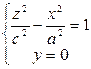и

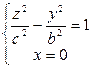
- гиперболы.

Пересечём плоскостью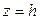

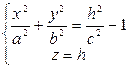- эллипс с полуосями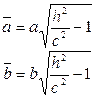

Полуоси возрастают с возрастанием 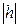, при 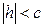поверхность с плоскостью не пересекается.

При 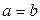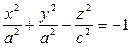- двуполосный гиперболоид вращения.

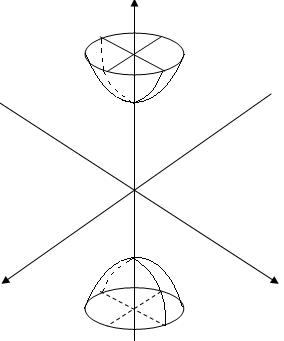
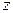
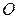
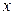
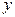
Параболоиды

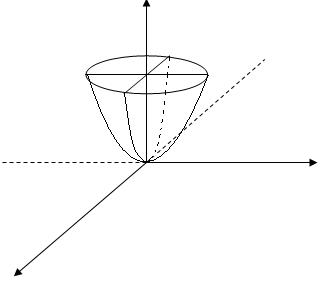
Эллиптический параболоид

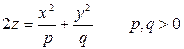
Пересекаем плоскостями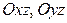

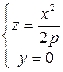
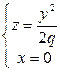
- параболы.

При пересечении плоскостью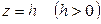

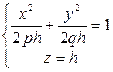- эллипс.

При 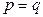получаем параболоид вращения.

⇐ Предыдущая 1 234 Следующая ⇒

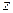
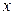
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.