
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Поверхности второго порядка.. Классификация алгебраических поверхностей второго порядка.. Уравнения и характеристические свойства поверхностей второго порядка.. Уравнение сферы.. Цилиндрические поверхности
Поверхности второго порядка.
Классификация алгебраических поверхностей второго порядка.
Уравнения и характеристические свойства поверхностей второго порядка.
Уравнение сферы.
Уравнение сферы:
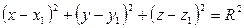
с центром в точке 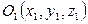 и радиусом
и радиусом 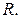 Раскроем скобки и, перенеся все члены в левую часть уравнения, получим:
Раскроем скобки и, перенеся все члены в левую часть уравнения, получим:
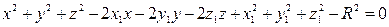 .
.
Это уравнение 2 степени относительно текущих координат 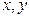 и
и 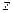 . В нём отсутствуют члены с произведением координат, а коэффициенты при
. В нём отсутствуют члены с произведением координат, а коэффициенты при 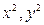 и
и 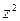 равны между собой.
равны между собой.
Любое уравнение второй степени относительно 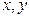 и
и 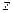 , в котором коэффициенты при
, в котором коэффициенты при 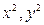 и
и 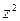 равны между собой, а члены с произведением координат отсутствуют, есть уравнение сферы.
равны между собой, а члены с произведением координат отсутствуют, есть уравнение сферы.
Если 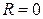 , то ему удовлетворяют координаты одной точки
, то ему удовлетворяют координаты одной точки 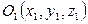 , если
, если 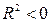 , то уравнение не определяет никакой поверхности.
, то уравнение не определяет никакой поверхности.
Цилиндрические поверхности
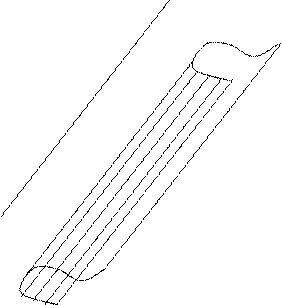
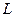
Поверхность, составленная из всех прямых, пересекающих данную линию 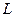 и параллельных данной прямой
и параллельных данной прямой 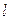 называется цилиндрической поверхностью. Линия
называется цилиндрической поверхностью. Линия 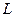 называется направляющей цилиндрической поверхности, а линия
называется направляющей цилиндрической поверхности, а линия 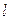 - образующей.
- образующей.
Не содержащее 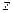 уравнение
уравнение 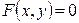 , если его отнести к системе координат в пространстве
, если его отнести к системе координат в пространстве 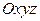 , является уравнением цилиндрической поверхности с образующими, параллельными оси
, является уравнением цилиндрической поверхности с образующими, параллельными оси 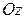 и направляющей
и направляющей 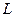 , которая в плоскости
, которая в плоскости 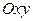 задаётся тем же уравнением
задаётся тем же уравнением 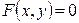 .
.
В пространстве 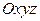 направляющая
направляющая 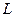 определяется системой двух уравнений:
определяется системой двух уравнений:
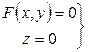 .
.
Уравнение 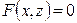 , не содержащее
, не содержащее 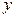 , и уравнение
, и уравнение 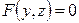 , не содержащие
, не содержащие 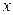 , определяют в пространстве
, определяют в пространстве 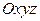 цилиндрические поверхности с образующими, параллельными соответственно осям
цилиндрические поверхности с образующими, параллельными соответственно осям 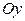 и
и 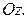
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|