Основные теоретические положения.

6. ПОВЕРХНОСТИ. СЕЧЕНИЕ ПОВЕРХНОСТЕЙ ПЛОСКОСТЯМИ ЧАСТНОГО ПОЛОЖЕНИЯ.

6.1. Основные теоретические положения.

Поверхность представляет собой множество последовательных положений линии, перемещающейся в пространстве. Эту линию называют образующей. Закон перемещения образующей может быть задан тоже линиями. Эти линии называются направляющими. Гранные поверхности образуются перемещением прямолинейной образующей L по ломаной направляющей. Поверхности вращения образуются вращением образующей L вокруг прямой i - оси вращения, при этом направляющими обычно являются окружностями.

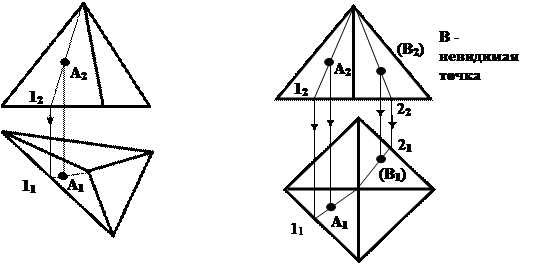Вид поверхности зависит от формы образующей линии и от закона перемещения ее в пространстве вдоль направляющей. Точку на гранной поверхности можно построить с помощью образующей, проходящей через эту точку (рис.82).

Рис.82.

Каждая точка образующей поверхности вращения описывает окружность, плоскость которой перпендикулярна оси вращения. Такие окружности называются параллелями. Кривые на поверхности вращения, образующиеся в результате пересечения поверхности вращения плоскостями, проходящими через ось вращения, называются меридианами. Строить точки на поверхности вращения удобнее всего с помощью параллелей (рис.83).

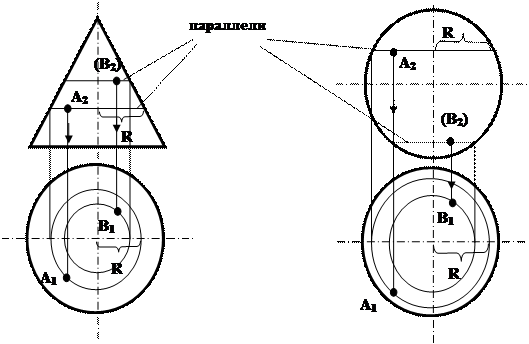Рис.83.

Линия сечения поверхности проецирующей плоскостью строится по точкам пересечения образующих поверхности или ее параллелей с плоскостью. Для гранных тел линией сечения будет ломаная, построенная на эпюре по точкам пересечения следа проецирующей плоскости с ребрами гранной поверхности. Если даны тела вращения, то для решения задачи нужно выбрать несколько, принадлежащих следу секущей плоскости, точек, провести через выбранные точки параллели (или образующие) , определить точки пересечения их со следом секущей плоскости; построить по ним лекальную кривую сечения. При этом в первую очередь следует определить характерные точки линии сечения на очерковых образующих (наиболее близкие, наиболее удаленные и др.).

12 3 4 5 Следующая ⇒