Главная

Контакты

Случайная статья

• Автоматизация
• Антропология
• Археология
• Архитектура
• Биология
• Ботаника
• Бухгалтерия
• Военная наука
• Генетика
• География
• Геология
• Демография
• Деревообработка
• Журналистика
• Зоология
• Изобретательство
• Информатика
• Искусство
• История
• Кинематография
• Компьютеризация
• Косметика
• Кулинария
• Культура
• Лексикология
• Лингвистика
• Литература
• Логика
• Маркетинг
• Математика
• Материаловедение
• Медицина
• Менеджмент
• Металлургия
• Метрология
• Механика
• Музыка
• Науковедение
• Образование
• Охрана Труда
• Педагогика
• Полиграфия
• Политология
• Право
• Предпринимательство
• Приборостроение
• Программирование
• Производство
• Промышленность
• Психология
• Радиосвязь
• Религия
• Риторика
• Социология
• Спорт
• Стандартизация
• Статистика
• Строительство
• Технологии
• Торговля
• Транспорт
• Фармакология
• Физика
• Физиология
• Философия
• Финансы
• Химия
• Хозяйство
• Черчение
• Экология
• Экономика
• Электроника
• Электротехника
• Энергетика

Построение линий пересечения поверхностей плоскостью

.

Рис. 18 б)

Построение линий пересечения поверхностей плоскостью

1. Пересечение многогранных тел плоскостью (общий случай).

Задачи на построение линии пересечения сводятся к построению точек пересечения прямых (ребер) с плоскостью или к нахождению линии пересечения плоскостей между собой. Чтобы найти одну точку, принадлежащую линии пересечения, нужно выполнить следующее построение:

1) провести вспомогательную секущую плоскость через ребро или грань;

2) найти линию пересечения вспомогательной секущей плоскости с заданной поверхностью;

3) определить искомые точки на пересечении найденных линий.

   Если задача будет решаться с помощью вспомогательных плоскостей, то последние ставят в такое положение, чтобы линия пересечения их с поверхностью проецировалась на плоскости проекций в виде простейших фигур, прямых или окружностей.

   Рассмотрим общий случай пересечения тела плоскостью (рис. 19). Даны треугольная пирамида SABC и плоскость α (DEF) общего положения. Требуется построить линию пересечения.

   Для решения применим алгоритм построения точки пересечения прямой с плоскостью. Заключим ребро SB во фронтально-проецирующую плоскость β и найдем линию пересечения этой плоскости с плоскостью DFE – прямую MN (M'N', M"N"). Эта линия пересечения пересечет ребро SB в точке 1 (1', 1") – следовательно, в этой точке ребро SB пересечет плоскость DFE – первой точке искомой линии пересечения.

   Аналогично заключим ребро SA во фронтально-проецирующую плоскость γ, которая в свою очередь пересечет плоскость DFE по прямой KL. Эта прямая пересечет ребро SA в точке 2 (2', 2") – точке пересечения ребра SA с плоскостью DFE – второй точке искомой линии пересечения.

   Заключим ребро SC во фронтально-проецирующую плоскость δ, которая пересечет плоскость DFE по прямой TH. Эта прямая пересечет ребро SC в точке 3 (3', 3") – точке пересечения ребра SC с плоскостью DFE – третьей точке искомой линии пересечения.

   Соединим последовательно полученные горизонтальные и фронтальные проекции точек 1, 2, 3: на горизонтальной плоскости сплошной (видимой) линией, т.к. все отрезки ломаной линии пересечения принадлежат видимым граням пирамиды, а на фронтальной плоскости – отрезки 1"-2", 2"-3" – сплошной (видимой), а отрезок 3"-1" – штриховой (невидимой) линией, т.к. он принадлежит невидимой грани ASB (A"S"B") на фронтальной плоскости.

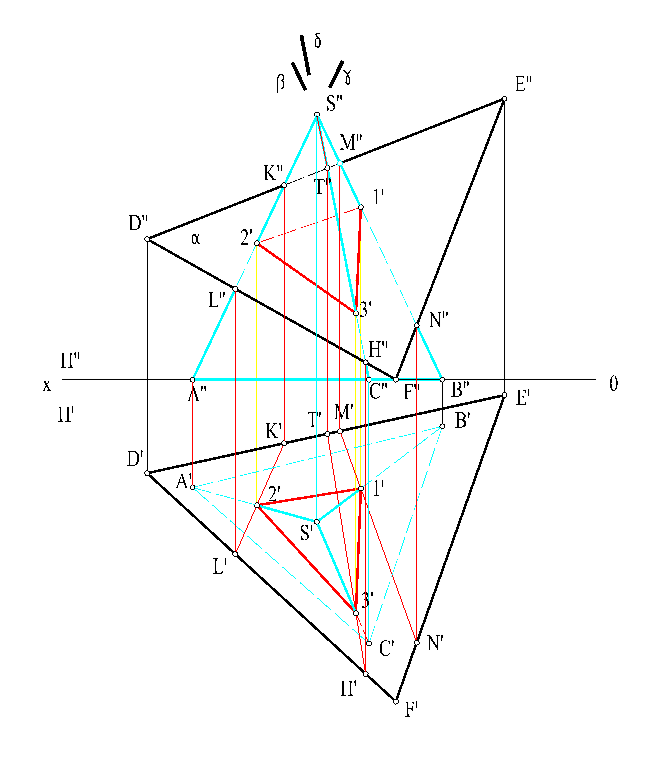
Рис. 19

   Для решения этой задачи можно применить один из способов преобразования чертежа, преобразовав плоскость общего положения в плоскость проецирующего положения.

   На чертеже (рис. 20) выполнено решение задачи с применением замены плоскостей проекций, где новая плоскость П₄ введена перпендикулярно горизонтальной плоскости П₁ и перпендикулярно горизонтали секущей плоскости DH (Х_{2 ┴} D'H'). В этом случае секущая плоскость DFE преобразуется из плоскости общего положения во фронтально-проецирующее. На чертеже видны точки линии пересечения 1, 2, 3 (1^IV,2^IV,3^IV), которые переносятся на первоначальный чертеж при помощи линий связи из условия принадлежности их соответствующим ребрам пирамиды .

   При пересечении поверхности геометрических тел плоскостями проецирующего положения одна проекция линии пересечения всегда будет частично или полностью совпадать с проекцией секущей плоскости: если плоскость горизонтально-проецирующая, то линия пересечения на горизонтальной плоскости совпадет с горизонтальной проекцией секущей плоскости. Если секущая плоскость фронтально-проецирующая, то линия пересечения совпадет с фронтальной проекцией плоскости и т.п.

   На чертежах (рис.21 и 22) приведены решения построения линий пересечения наклонных призмы и пирамиды секущими плоскостями фронтально-проецирующего положения. На фронтальной плоскости линия пересечения совпала с фронтальным следом секущей плоскости Q_П". Горизонтальная проекция линии пересечения достраивается по линиям связи из условия принадлежности точек ребрам призмы или пирамиды.

   Поскольку секущая плоскость пересекает все три ребра боковой поверхности призмы (или пирамиды), в сечении получаем треугольник.

   Видимость линий пересечения определяется видимостью граней многогранников: если участок линии пересечения принадлежит видимой грани, то он видимый, если принадлежит невидимой – невидимый.

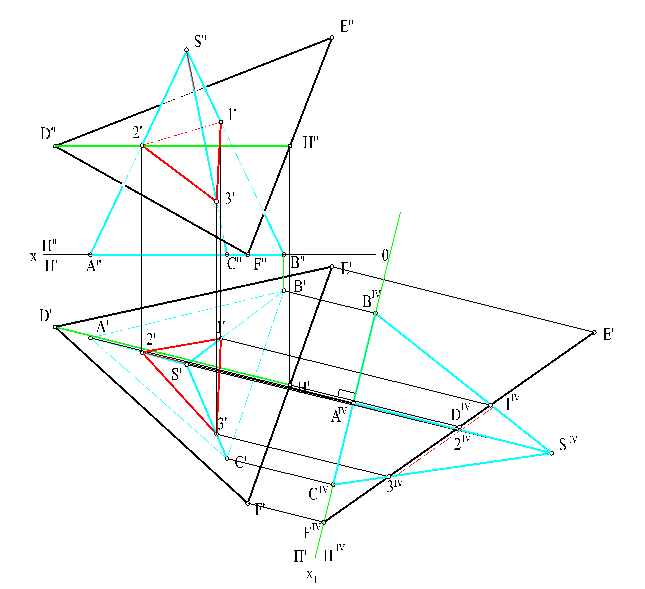
Рис. 20

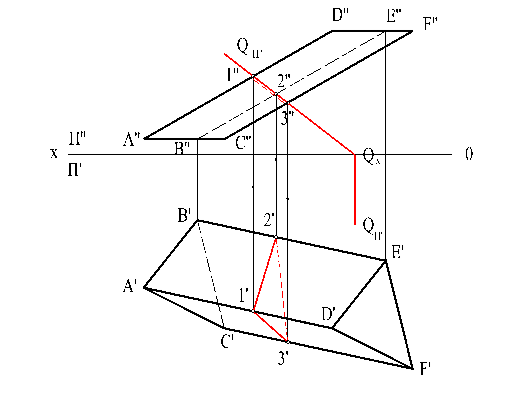
Рис. 21

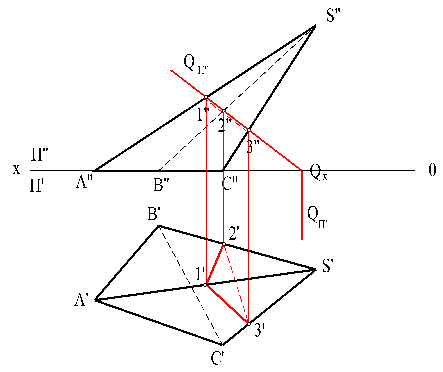
Рис. 22

1. Пересечение тел вращения проецирующей плоскостью.

   При пересечении тела вращения плоскостью контур пересечения будет представлять собой замкнутую плоскую кривую линию, форма которой зависит от формы тела вращения и положения секущей плоскости относительно оси вращения. Это может быть окружность, эллипс. парабола, гипербола, а также различные сложные сочетания кривых линий.

   Чтобы построить линию пересечения поверхности вращения секущей плоскостью, необходимо построить ряд точек, которые будут принадлежать и поверхности тела вращения, и плоскости. Построение следует начинать с характерных точек. К таким точкам относятся: габаритные точки, определяющие наибольшие размеры линии пересечения по высоте и ширине; точки, лежащие на крайних образующих и образующих, проекции которых совпадают с осевыми линиями. По расположению этих точек можно представить характер искомой линии пересечения.

   Построив характерные точки, строят промежуточные точки, используя для этого в качестве вспомогательных линий прямые – образующие или окружности (меридианы и параллели). Строя линию пересечения, необходимо знать, по какой кривой пересекаются тела вращения – цилиндр, конус, шар (сфера) и тор.

а) Пересечение прямого кругового цилиндра проецирующей плоскостью.

   Если прямой круговой цилиндр пересечь плоскостью, перпендикулярной оси вращения, то линия пересечения боковой поверхности с этой плоскостью будет окружность (рис. 23).

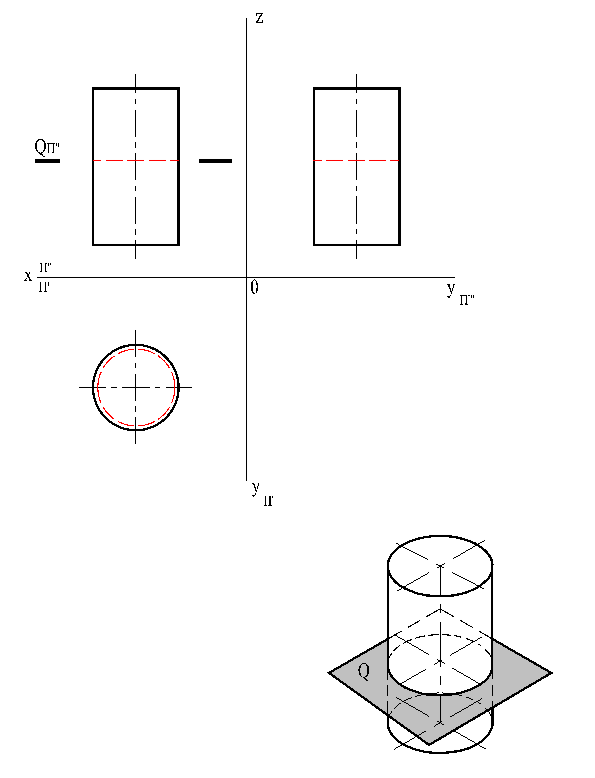
Рис. 23

   Если цилиндр пересечь наклонной плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности с этой плоскостью будет эллипсом, величина и форма которого зависят от угла наклона секущей плоскости к плоскостям оснований цилиндра (рис. 24).

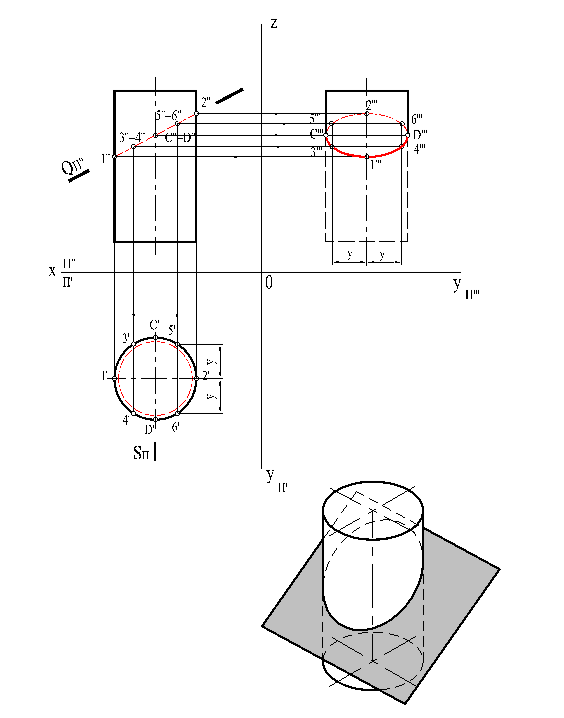
Рис. 24

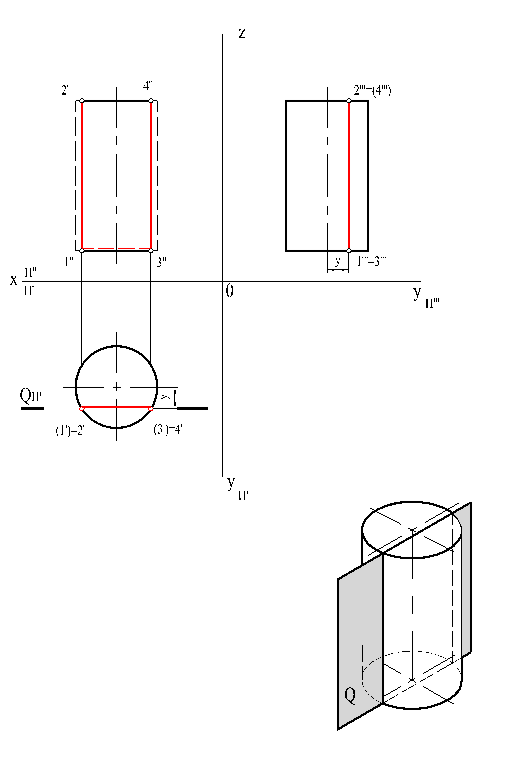
Рис. 25

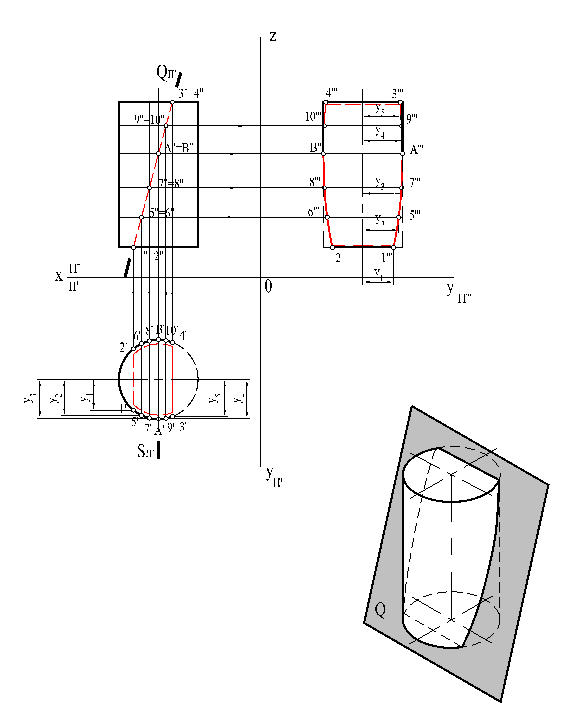
Рис. 26

        Если цилиндр пересечь плоскостью, перпендикулярной к его основаниям, линия пересечения боковой поверхности с этой плоскостью будет прямоугольником (рис. 25).

   Если цилиндр пересечь наклонной плоскостью так, что она пересечет основания и боковую поверхность, то линия пересечения будет частью эллипса, отсеченной двумя хордами оснований (рис. 26).

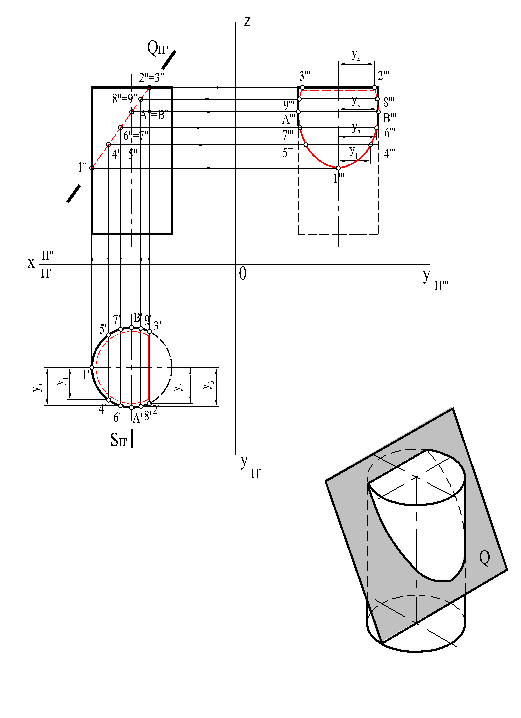
Рис. 27

   Если секущая плоскость пересечет одно основание и часть боковой поверхности, то линия пересечения боковой поверхности с этой плоскостью будет частью эллипса, отсеченного одной хордой основания.

б) Пересечение прямого кругового конуса проецирующей плоскостью

   На чертежах ниже (рис. 28-32) приведены примеры пересечения прямого кругового конуса плоскостями различного положения, где каждому наглядному изображению соответствует фронтальная проекция конуса со следом фронтально-проецирующей секущей плоскости.

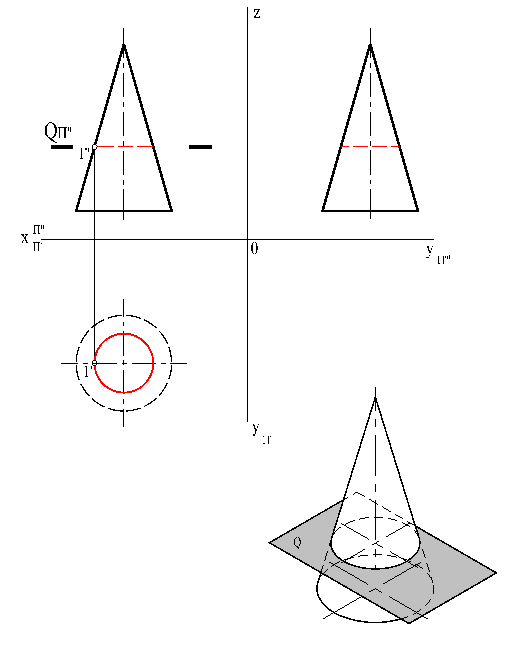
    Рис. 28

   Если прямой круговой конус пересечь плоскостью, параллельной основанию, то линия пересечения боковой поверхности конуса с плоскостью будет окружностью (рис. 28).

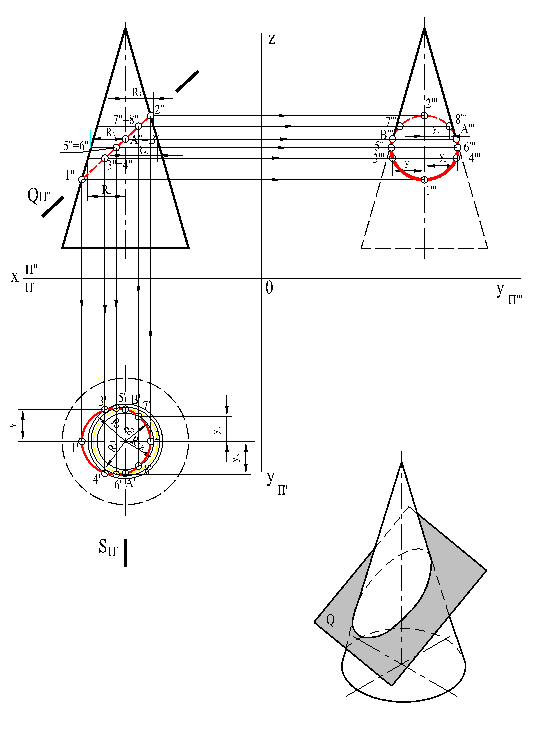
Рис.29

   Если конус пересечь наклонной секущей плоскостью так, чтобы пересеклись все его образующие, то линия пересечения боковой поверхности конуса с плоскостью будет эллипсом (рис. 29).

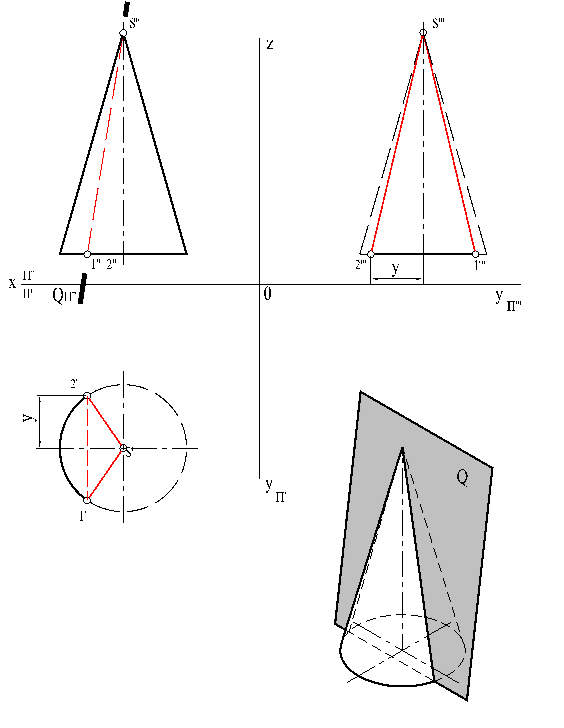Рис. 30

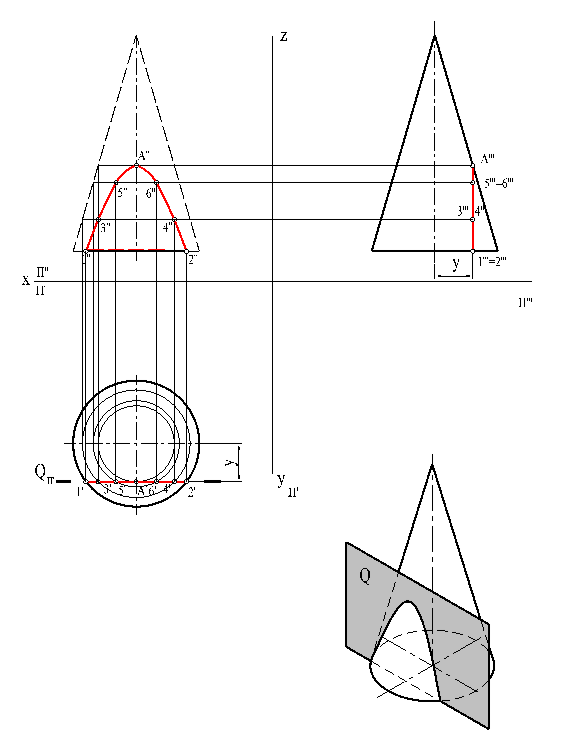
   Если такой конус пересечь плоскостью, которая пройдет через его вершину, то, будет ли плоскость перпендикулярна или наклонна к основанию конуса, линия пересечения боковой поверхности конуса с 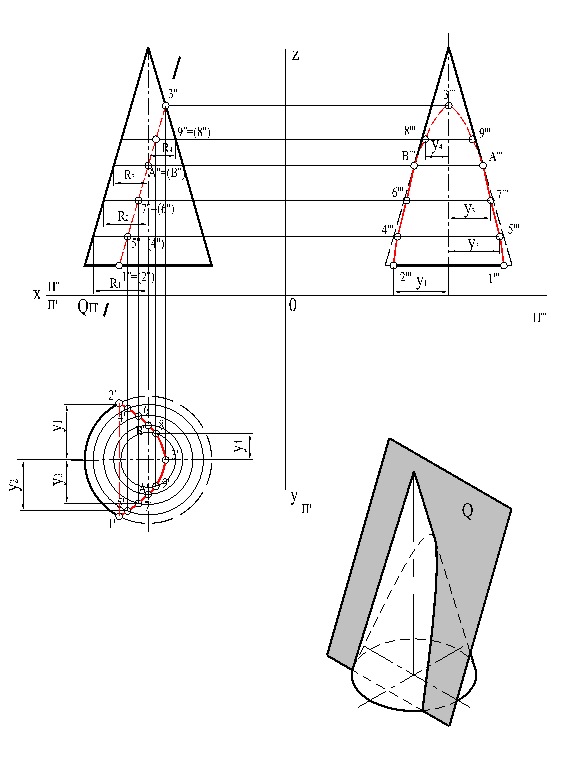плоскостью будет треугольником (рис. 30).

Рис. 31

Если боковую поверхность прямого кругового конуса пересечь плоскостью так, чтобы она была параллельна сразу двум образующим, то линия пересечения боковой поверхности с плоскостью будет параболой (рис. 31).

Рис.32

   Если боковую поверхность прямого кругового конуса пересечь плоскостью так, чтобы она была перпендикулярна основанию конуса, то линия пересечения боковой поверхности с плоскостью будет гиперболой (рис. 32).

в) пересечение сферы проецирующей плоскостью

Сфера представляет собой единственную геометрическую поверхность, которая при пересечении плоскостью в любом направлении дает линию пересечения в виде окружности.

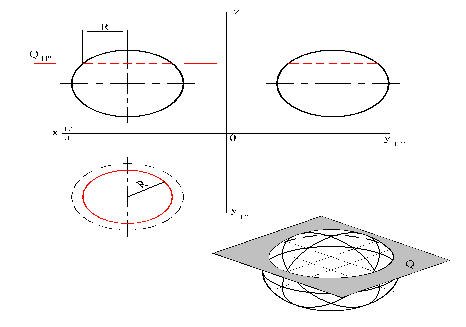
Рис. 33

   Секущие плоскости, проходящие через вертикальную ось сферы, пересекают ее по меридианам. Если секущие плоскости пересекают сферу перпендикулярно вертикальной оси вращения, то в пересечении получаем окружности – параллели.

   На чертеже (рис. 33) изображена сфера в трех проекциях, которую пересекает плоскость, занимающая горизонтальное положение. Эта плоскость пересечет сферу по окружности – параллели. На фронтальной и профильной плоскостях проекций эта линия пересечения в виде отрезка прямой, совпадающей со следом секущей плоскости, на горизонтальной плоскости – в виде окружности соответствующего радиуса.

   Если сферу пересекать проецирующей наклонной плоскостью (рис. 34), то в пересечении все равно будет получаться окружность, но проецироваться эта окружность будет на одну плоскость в виде отрезка прямой, совпадающей со следом секущей плоскости, а на другие плоскости проекций – в виде эллипсов.

   Построение эллипса начинают с характерных точек, которыми будут концы большой и малой оси, а также точек видимости.

Рис. 34

в) пересечение торовой поверхности проецирующей плоскостью.

Рис. 35

   Если секущая плоскость расположена перпендикулярно оси вращения торовой поверхности и параллельна горизонтальной плоскости проекций, то в сечении будет получаться окружность.