АЛГЕБРА. Метод интервалов

АЛГЕБРА

Метод интервалов

Суть метода состоит в том, что числовая ось разбивается на интервалы (промежутки) таким образом, что в пределах одного промежутка исследуемое выражение сохраняет постоянный знак.

Рассмотрим выражение А= 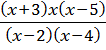и выясним, какие знаки оно имеет при различных значениях х.

Корни числителя 3, 0 и 5 (то есть числа, при подстановке которых в выражение вместо х, числитель обращается в 0) и знаменателя 2 и 4, разбивают действительную ось на интервалы:

-3 0 2 4 5

Нетрудно видеть, что при х 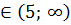(то есть при 5<x< 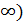все множители, входящие в выражение А – положительны, и значит А>0. При х 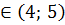множитель (х-5) становится меньше 0, а все остальные множители сохраняют прежний знак, и значит А меняет знак на противоположный: А<0. При переходе в следующий интервал х 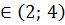знак изменит только один множитель 1/(х-4), а все остальные множители сохранят прежний знак, и значит А снова изменит знак на противоположный и станет больше 0: А>0.

Таким образом, в пределах одного интервала выражение А сохраняет знак постоянным, поскольку сохраняют знак постоянным все множители, входящие в выражение. Например, 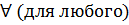х 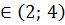знак А постоянный и А>0, так как 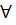х 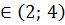1/(х-4) и (х-5) меньше 0, а все остальные множители больше 0.

При переходе в смежный интервал знак А меняется на противоположный, поскольку меняет знак только один множитель.

Получаем, что А>0 при 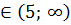х 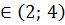, х , х 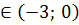(Равносильная запись: 5<x< 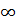, 2<x<4, -3<x<0). А<0 при 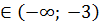х 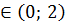, х , х 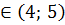. Интервалы, в которых А<0 выделены жирной линией.

Предположим теперь, что множители, входящие в выражение имеют степени, отличные от 1.

Пусть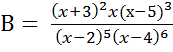

Разобьём числовую ось на те же интервалы и заметим, что в пределах одного интервала выражение В сохраняет знак постоянным, поскольку как и в предыдущем случае сохраняют знак постоянным все множители, входящие в выражение.

Различие в том, что при переходе из интервала (4; 5) в интервал (2; 4) и из интервала (0; -3) в интервал ( 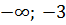) знак В не меняется, так как не меняется знак множителей 1/(х-4)⁶>0 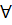x и (х+3)²>0 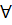x.

Остальные множители: х, (х-5)³, 1/(х-2)⁵ при переходах в соседние интервалы соответственно через 0, 5 и 2, меняют знак на противоположный. Следовательно, меняет знак и выражение В

-3 0 2 4 5

В отрицательно на интервалах, выделенных жирной линией, кроме точек -3 и 4 – в них В=0, и положительно на оставшейся части оси.

12 3 Следующая ⇒