Контактная разность потенциалов

Контактная разность потенциалов

Рассмотрим теперь контакт двух металлов с разной концентрацией электронов в зоне проводимости (например, n₁>n₂) и соответственно с разными расположениями в ней уровня Ферми (E_F₁располагается тогда выше E_F₂в соответствии с формулой (1)). Если для начала допустить, что абсолютная температура металлов равна нулю, то мы имеем дело в месте контакта со скачками как концентрации электронов, так и уровней Ферми, причем переходам электронов из металла с большей их концентрацией в металл с меньшей концентрацией запрещено происходить вследствие отсутствия теплового движения электронов и того факта, что если допустить эти переходы, то немедленно возникнет возвращающее электрическое поле бесконечно большой напряженности. На основании этих рассуждений мы вынуждены утверждать сохранность исходных расположений уровней Ферми при вхождении металлов в контакт, что находится однако в противоречии с представлениями многих авторов работ по зонной теории металлов, утверждающих обязательное выравнивание уровней Ферми в условиях контакта. Таким образом, следуя нашим представлениям, контактной разности потенциалов двух разнородных металлов, связанной с разницей их уровней Ферми, равно как и с разницей работ выхода электронов из них, не должно существовать. Именно эта же позиция просматривается в учебнике [2] (в отличии от [1] ), где излагается наиболее правильная с нашей точки зрения теория контактной разности потенциалов двух разных металлов. Однако и в нем не дана полная и детализированная теория этих явлений, хотя она видится нам как наиболее корректная.

Рассмотрим суть этой теории, снабдив ее дополнительно нашими представлениями о происходящих явлениях. Итак, еще раз подчеркнем, что контактной разности потенциалов двух разнородных металлов при абсолютном нуле их температуры не существует. Другое дело, если температура обоих металлов в окрестности контакта конечна и, более того, одинакова. Электроны проводимости в этом случае принимают участие в хаотическом (т.е. тепловом) движении, и в месте контакта возникает их предпочтительная диффузия из металла с большей концентрацией в металл с меньшей концентрацией. Диффузия приводит к “сглаживанию” скачка концентрации электронов проводимости в узкой области контакта, который существовал бы при абсолютном нуле температуры. С другой стороны этой диффузии противодействует электрическое поле, возникающее в области контакта за счет появления некомпенсированных разноименных заряженных областей, расположенных по разные стороны контактной поверхности, причем это возникновение происходит в соответствии с уравнением Пуассона:

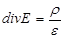
(3)

где 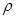- объемная плотность нескомпенсированного заряда в окрестности контакта, 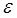- диэлектрическая проницаемость среды. От напряженности электрического поля Е можно перейти к распределению потенциала φ вдоль линии, перпендикулярной поверхности контакта согласно уравнению

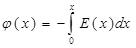(4)

что подчеркивает и здесь сходство такого потенциала с понятием «внешнего» потенциала, использованного нами при рассмотрении металлов в обособленном виде (см. рис.1 и рис.2). Важно здесь отметить, что при определенной температуре устанавливается динамическое равновесие процессов диффузии электронов и процессов рождения электрического поля в области контакта и контактной разности потенциалов. Это равновесие приводит к самосогласованным распределениям 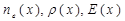и 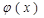, вид которых качественно представлен на рис.3.

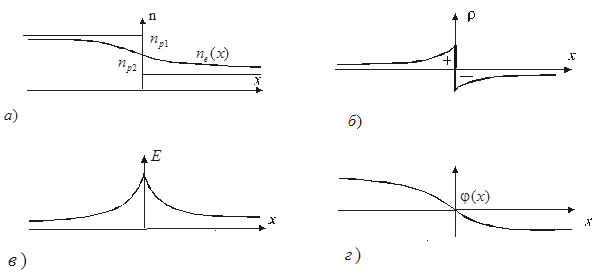
рис. 3. Распределение концентрации зарядов (а), нескомпенсированной плотности зарядов (б), напряженности электрического поля (в) и электрического потенциала (г) в окрестности контакта двух разнородных металлов в условиях его конечной абсолютной температуры.

Важно здесь иметь ввиду, что с ростом температуры область «сглаживания» скачка концентрации электронов в окрестности контакта расширяется, что ведет к росту области существования и высоты скачка на контакте плотности неcкомпенсированного заряда, к расширению и увеличению значений положительного электрического поля и, наконец, к увеличению контактной разности потенциалов. Причем последняя может трактоваться как электродвижущая сила, порожденная разницей исходных концентраций электронов в соприкасающихся металлах и процессами предпочтительной диффузии электронов из металла с большей концентрацией в металл с меньшей концентрацией (сторонняя сила).

Для того, чтобы облечь приведенные качественные представления в количественную форму, обратимся к теории, которая представлена в упомянутом уже учебнике [2] и которая наиболее близко соответствует приведенным представлениям. Рассмотрим вновь контакт двух металлов с разной концентрацией электронов (n₁>n₂). Поскольку в месте их контакта оба металла имеют одинаковую температуру, то и средняя скорость теплового движения в этом месте одна и та же. Для простоты рассуждения положим, что длина свободного пробега у них одинакова. За счет теплового движения электронов происходит их диффузия. Число электронов, которые переносятся из первого металла во второй через площадку S равно одной шестой числа электронов, находящихся в слое толщиной λ, т.е. 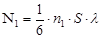. Из второго металла в первый переносится 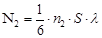электронов. Но по условию 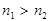, следовательно, второй металл приобретет больше электронов, чем он отдаст первому. Этот процесс можно описать с помощью т.н. диффузионного тока, текущего через контакт например слева направо

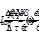(5)

Здесь 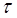и u есть соответственно среднее время свободного пробега и средняя скорость теплового движения электронов. В противоположную сторону течет ток проводимости I_e , обусловленный возникшей разностью потенциалов ∆φ_e, которая и является предметом определения.

Согласно закону Ома I=∆φ/R, где R есть сопротивление приконтактной области R, которое можно приближенно определить как:

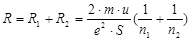(6)

В условиях установившегося состояния I_e=I_диф., и тогда

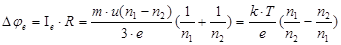(7)

Мы видим, что возникшая контактная разность потенциалов зависит здесь

только от абсолютной температуры и рода металлов, различающихся концентрациями свободных электронов.

⇐ Предыдущая 1 234 5 6 Следующая ⇒