
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Уравнение плоскости
2. Уравнение плоскости
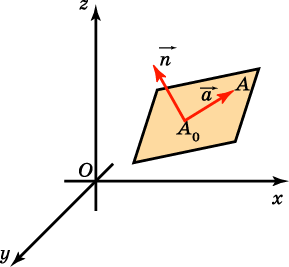 Для вывода уравнения плоскости воспользуемся условием перпендикулярности векторов. Рассмотрим плоскость
Для вывода уравнения плоскости воспользуемся условием перпендикулярности векторов. Рассмотрим плоскость 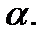 Пусть точка
Пусть точка 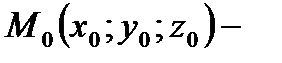 известная точка, принадлежащая данной плоскости, и пусть вектор
известная точка, принадлежащая данной плоскости, и пусть вектор 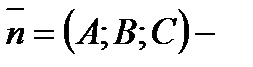 известный вектор, перпендикулярный плоскости
известный вектор, перпендикулярный плоскости 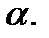 Такой вектор называется нормальным вектором (нормалью) плоскости. Точка
Такой вектор называется нормальным вектором (нормалью) плоскости. Точка 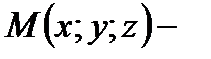 произвольная точка пространства. Для того, чтобы выполнялось условие
произвольная точка пространства. Для того, чтобы выполнялось условие 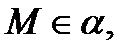 необходимо и достаточно, чтобы вектора
необходимо и достаточно, чтобы вектора 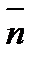 и
и 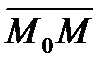 были перпендикулярны, следовательно, скалярное произведение этих векторов должно быть равно
были перпендикулярны, следовательно, скалярное произведение этих векторов должно быть равно 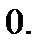
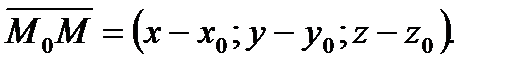
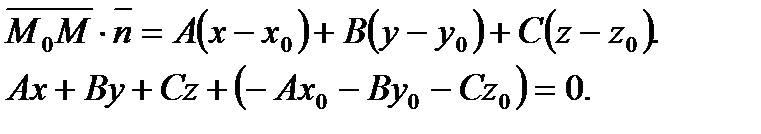
Обозначим 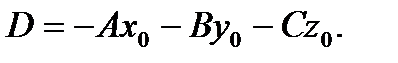 Отсюда
Отсюда 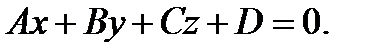 Полученное уравнение является уравнением плоскости
Полученное уравнение является уравнением плоскости 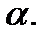
Задача 3
Написать уравнение плоскости, проходящей через середину отрезка 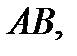 перпендикулярно к нему, если
перпендикулярно к нему, если 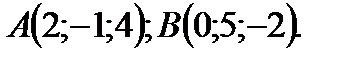
Решение
Найдём координаты точки 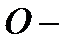 середины отрезка
середины отрезка 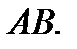
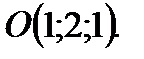
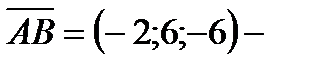 нормальный вектор искомой плоскости.
нормальный вектор искомой плоскости.
Отсюда искомое уравнение имеет вид 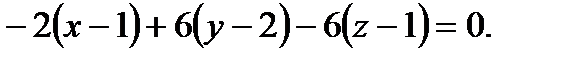
Итак, 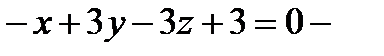 искомое уравнение.
искомое уравнение.
Задача 4
Написать уравнение плоскости, проходящей через начало координат, перпендикулярно прямой 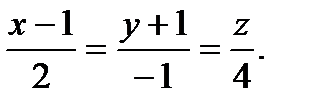
Решение
Направляющий вектор данной прямой будет нормалью к искомой плоскости, следовательно, 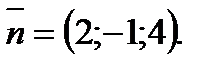 Тогда уравнение плоскости имеет вид
Тогда уравнение плоскости имеет вид 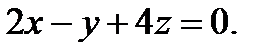
Задача 5
Написать уравнение плоскости, проходящей через точки 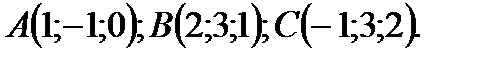
Решение
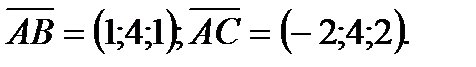 Так как координаты найденных векторов не являются пропорциональными, то
Так как координаты найденных векторов не являются пропорциональными, то 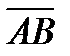 и
и 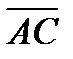 неколллинеарны, а значит, точки
неколллинеарны, а значит, точки 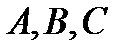 не лежат на одной прямой. Через три точки, не лежащие на одной прямой можно провести единственную плоскость. Нормальный вектор этой плоскости должен быть перпендикулярен любому вектору, лежащему в плоскости, а по критерию перпендикулярности прямой и плоскости для этого необходимо и достаточно перпендикулярности каким-либо двум неколлинеарным векторам, лежащим в плоскости. Пусть нормаль
не лежат на одной прямой. Через три точки, не лежащие на одной прямой можно провести единственную плоскость. Нормальный вектор этой плоскости должен быть перпендикулярен любому вектору, лежащему в плоскости, а по критерию перпендикулярности прямой и плоскости для этого необходимо и достаточно перпендикулярности каким-либо двум неколлинеарным векторам, лежащим в плоскости. Пусть нормаль 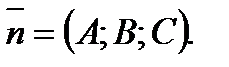 Тогда
Тогда 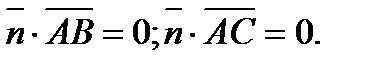
Найдём координаты нормали из системы
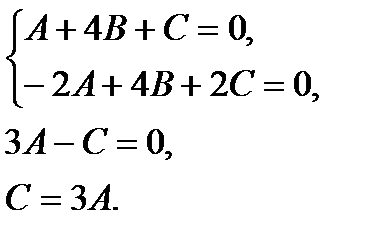
Пусть 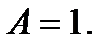 Тогда
Тогда 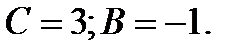
Таким образом 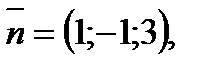 а уравнение искомой плоскости имеет вид
а уравнение искомой плоскости имеет вид 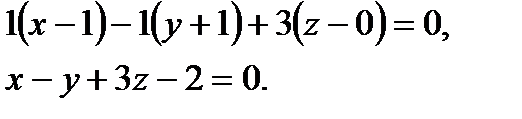
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|