
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры задач. Размещения. Примеры
Примеры задач
— Таким образом , число всевозможных перестановок из n элементов вычисляется по формуле: Рn=n!
— Пример 1. Сколькими способами могут быть расставлены 8 участниц финального забега на восьми беговых дорожках?
— Р8=8!=40320
— Пример 2. Сколько различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?
— Из цифр 0,2,4,6 можно получить Р4 перестановок. Из этого числа надо исключить те перестановки , которые начинаются с 0.Получаем: Р4-Р3=4!-3!=18
Размещения
Пусть имеется 4 шара и 3 пустых ячейки . В пустые ячейки можно по-разному разместить три шара из этого набора шаров . Выбирая разными способами первый , второй и третий шары , будем получать различные тройки шаров.
Каждую упорядоченную тройку , которую можно составить из четырех элементов , называют размещением из четырех элементов по три
— Размещением из n элементов по к (к<n) называется любое множество , состоящее из любых к элементов , взятых в определенном порядке из данных n элементов
— Число размещений из n элементов по к обозначают
— Читают « А из n по к »
— 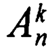
— 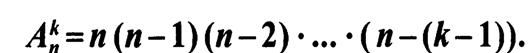
Примеры
— 1. Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
В этом примере речь идет о размещениях из 8 элементов по 4. Имеем: 
— 1. Учащиеся второго класса изучают 8 предметов. Сколькими способами можно составить расписание на один день, чтобы в нем было 4 различных предмета?
В этом примере речь идет о размещениях из 8 элементов по 4. Имеем:
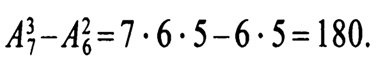
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|