
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Примеры комбинаторных задач. Перестановки
Алгебра 9 класс 27.05 учитель Оверченко Г.Л.
Тема урока: «Элементы комбинаторики и теории вероятностей. (повторение)»
Примеры комбинаторных задач
— Задачи , решая которые приходится составлять различные комбинации из конечного числа элементов и подсчитывать число комбинаций , называются комбинаторными
— Раздел математики , в котором рассматриваются подобные задачи, называют комбинаторикой
— Слово «комбинаторика» от латинского combinare - «соединять , сочетать»
1.Из группы теннисистов, в которую входят четыре человека-Антонов, Григорьев , Сергеев и Федоров , тренер выделяет пару для участия в соревнованиях . Сколько существует вариантов выбора такой пары?
АГ, АС, АФ
ГС, ГФ
СФ
Значит, всего существует шесть вариантов выбора
Способ рассуждений , которым мы воспользовались , называют перебором возможных вариантов
Сколько трехзначных чисел можно составить из цифр 1, 3, 5, 7 ,используя в записи числа каждую из них не более
одного раза?
2. Чтобы ответить на вопрос задачи , выпишем все такие числа . Полученные результаты запишем в четыре строки , в каждой из которых шесть чисел:
135 137 153 157 173 175
315 317 351 357 371 375
513 517 531 537 571 573
713 715 731 735 751 753
Перестановки
— Простейшими комбинациями , которые можно составить из элементов конечного множества , являются перестановки
— Число перестановок из n элементов обозначают символом Рn(читается «Р из n»)
— Для произведения первых n натуральных чисел используют специальное обозначение: n! ( читается n факториал)
— 2!=2; 5!=120; 1!=1
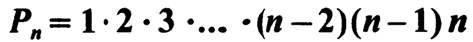
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|