
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Аномалии Вуда – Рэлея
Аномалии Вуда – Рэлея
Коллективные решеточные резонансы появляются на длинах волн, близких (слегка смещенных в красную сторону) к аномалиям Вуда – Рэлея, что в общем случае регулярной двумерной решетки (с шагом 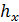 и
и 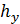 вдоль осей
вдоль осей 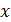 и
и 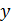 ) имеет место быть, если:
) имеет место быть, если:
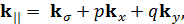
| (3) |
где 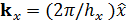 и
и 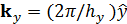 – векторы обратной решетки,
– векторы обратной решетки, 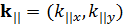 – волновой вектор волны, распространяющейся в плоскости решетки,
– волновой вектор волны, распространяющейся в плоскости решетки, 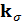 – проекция падения волнового вектора на плоскости решетки,
– проекция падения волнового вектора на плоскости решетки, 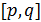 представляет собой пару целых чисел, которые обозначают порядок аномалии, а
представляет собой пару целых чисел, которые обозначают порядок аномалии, а 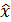 и
и 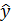 – обозначает единичный вектор. Явно, компоненты
– обозначает единичный вектор. Явно, компоненты 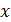 и
и 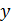 в уравнении (3) читаются как:
в уравнении (3) читаются как:
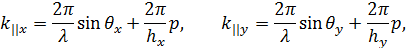
| (4) |
где 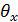 и
и 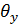 – углы между осью
– углы между осью 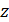 и проекциями
и проекциями 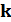 на плоскости XOZ и YOZ.
на плоскости XOZ и YOZ.
В однородной среде волновой вектор волны, распространяющейся в плоскости решетки, равен 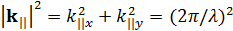 , что наряду с уравнениями (4) дает квадратное уравнение для
, что наряду с уравнениями (4) дает квадратное уравнение для 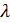 :
:
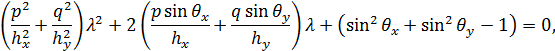
| (4) |
где для данной комбинации целых чисел 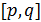 можно получить соответствующую спектральную позицию
можно получить соответствующую спектральную позицию 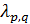 для аномалии Вуда – Рэлея порядка
для аномалии Вуда – Рэлея порядка 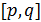 .
.
Для специального случая нормального падения ( 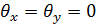 ) эти аномалии Вуда – Рэлея просто равны длине полны
) эти аномалии Вуда – Рэлея просто равны длине полны 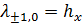 и
и 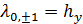 . Однако уравнение (5) сразу подразумевает, что широкий разброс
. Однако уравнение (5) сразу подразумевает, что широкий разброс 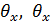 может привести к появлению КРР, возникающих в результате гибридизации с аномалиями Вуда – Рэлея более высокого порядка (т.е.
может привести к появлению КРР, возникающих в результате гибридизации с аномалиями Вуда – Рэлея более высокого порядка (т.е. 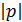 ,
, 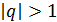 ).
).
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|