Модель связанных диполей

Модель связанных диполей

Рассмотрим решетку из сферических наночастиц с конечным количеством частиц 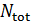, находящихся в вакууме и освещенных плоской волной, где в любом месте 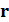, можно записать уравнение:

где – 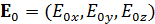и 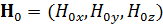амплитуды электрического и магнитного полей, а 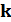- волновой вектор. В рамках точечно-дипольного приближения электрические 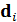и магнитные 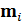дипольные моменты, индуцированные на i-ых наночастицах при таком падении, связаны с соответствующими диполями на других 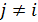наночастицах и с внешним полем:

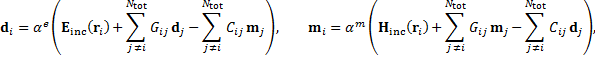
(1)

где 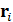– положение -ой наночастиц, соответствующие центру решетк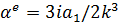и, и 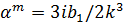электрическая и магнитная дипольная поляризуемость, где 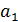и 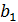– коэффициенты рассеяния, 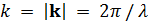, где 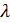– длина волны.

Тензоры 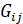и 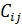описывают взаимодействие между диполями, индуцированные на 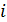-ой и 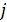-ой наночастице:

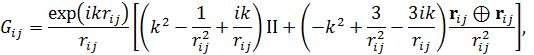
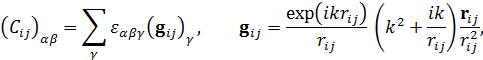
где II – тензор 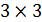компоненты, 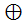обозначает тензорное произведение, 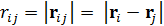– меж центровое расстояние между -ой и 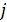-ой НЧ, а 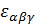– символ Леви-Чивиты с 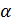, , 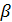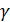обозначает декартовы компоненты тензоров.

Для решетки с заданной геометрией и составом наночастиц, решение линейной системы уравнений (1) дает 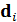и , и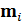ндуцированные на каждой -ой НЧ; таким образом, электромагнитный отклик решетки на падающее возбуждение может быть явно найдено. В частности, в этой работе мы рассматриваем общее количество электромагнитной энергии, рассеянной и поглощенной решеткой, нормированной на сумму площади поперечного сечения всех наночастиц, то есть эффективности затухания:

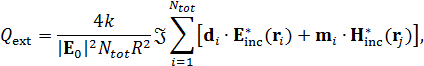
(2)

где звездочка обозначает комплексное сопряжение, 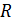– радиус наночастиц, и 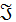принимает мнимую часть.

⇐ Предыдущая 123 4 5 Следующая ⇒