
- Автоматизация
- Антропология
- Археология
- Архитектура
- Биология
- Ботаника
- Бухгалтерия
- Военная наука
- Генетика
- География
- Геология
- Демография
- Деревообработка
- Журналистика
- Зоология
- Изобретательство
- Информатика
- Искусство
- История
- Кинематография
- Компьютеризация
- Косметика
- Кулинария
- Культура
- Лексикология
- Лингвистика
- Литература
- Логика
- Маркетинг
- Математика
- Материаловедение
- Медицина
- Менеджмент
- Металлургия
- Метрология
- Механика
- Музыка
- Науковедение
- Образование
- Охрана Труда
- Педагогика
- Полиграфия
- Политология
- Право
- Предпринимательство
- Приборостроение
- Программирование
- Производство
- Промышленность
- Психология
- Радиосвязь
- Религия
- Риторика
- Социология
- Спорт
- Стандартизация
- Статистика
- Строительство
- Технологии
- Торговля
- Транспорт
- Фармакология
- Физика
- Физиология
- Философия
- Финансы
- Химия
- Хозяйство
- Черчение
- Экология
- Экономика
- Электроника
- Электротехника
- Энергетика
Методы уточнения корня уравнения
4.2. Методы уточнения корня уравнения
Пусть 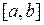 – промежуток изоляции корня уравнения
– промежуток изоляции корня уравнения 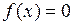 в случае, когда функция
в случае, когда функция 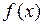 непрерывна на этом отрезке. Конкретизируем условия, которым должна удовлетворять функция
непрерывна на этом отрезке. Конкретизируем условия, которым должна удовлетворять функция 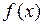 , чтобы постановка задачи приближенного решения уравнения оказалась корректной:
, чтобы постановка задачи приближенного решения уравнения оказалась корректной:
1) 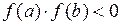 (это означает, что на отрезке
(это означает, что на отрезке 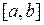 содержится корень уравнения – в соответствии с теоремой Больцано-Коши);
содержится корень уравнения – в соответствии с теоремой Больцано-Коши);
2) производные 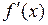 и
и 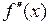 сохраняют свой знак на всём отрезке
сохраняют свой знак на всём отрезке 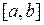 (это означает, что функция
(это означает, что функция 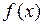 монотонна и не меняет характер выпуклости на промежутке
монотонна и не меняет характер выпуклости на промежутке 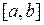 ).
).
Возможны два варианта соотношения знаков указанных выше производных:
(I) 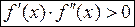 на отрезке
на отрезке 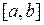 (по-другому:
(по-другому: 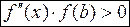 )
)
или
(II) 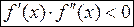 на отрезке
на отрезке 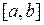 (по-другому:
(по-другому: 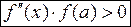 ).
).
Рассмотрим так называемый метод касательных (Ньютона), предназначенный для нахождения приближенного значения корня, геометрический смысл которого состоит в замене на каждом шаге дуги кривой 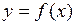 , заданной на отрезке
, заданной на отрезке 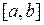 , касательной к ней и нахождение точек пересечения полученных касательных с осью (Оx). Для случая (I), например, строим касательную (К1) к графику функции
, касательной к ней и нахождение точек пересечения полученных касательных с осью (Оx). Для случая (I), например, строим касательную (К1) к графику функции 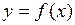 в точке с абсциссой
в точке с абсциссой 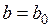 и находим абсциссу
и находим абсциссу 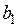 точки пересечения этой касательной с осью (Оx), затем строим касательную (К2) в точке графика
точки пересечения этой касательной с осью (Оx), затем строим касательную (К2) в точке графика 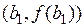 и находим абсциссу
и находим абсциссу 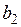 точки пересечения касательной (К2) с осью (Оx), и так далее (рис. 20).
точки пересечения касательной (К2) с осью (Оx), и так далее (рис. 20).
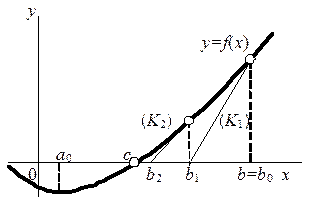
Рис. 20
Очевидно, что каждое значение 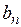 , полученное на n-ом шаге (n = 0, 1, 2, …), является приближённым значением корня данного уравнения (для случая (I) – с недостатком). Для нахождения этих приближённых значений составим уравнение касательной (Кn), проходящей через точку графика с координатами
, полученное на n-ом шаге (n = 0, 1, 2, …), является приближённым значением корня данного уравнения (для случая (I) – с недостатком). Для нахождения этих приближённых значений составим уравнение касательной (Кn), проходящей через точку графика с координатами 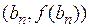 :
: 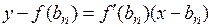 , после чего определим абсциссу точки пересечения касательной с осью (Оx). Учитывая, что
, после чего определим абсциссу точки пересечения касательной с осью (Оx). Учитывая, что 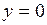 , получим
, получим
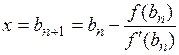 (n = 0, 1, 2, 3, …).
(n = 0, 1, 2, 3, …).
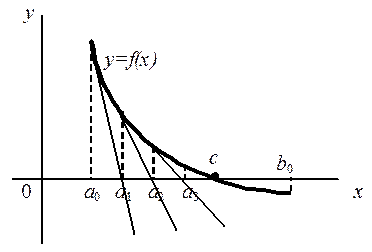
Рис. 21
Это и есть так называемая рекуррентная формула метода касательных, с помощью которой можно найти приближённое значение корня (с избытком).
В случае (II)аналогично выводится рекуррентная формула метода касательных, позволяющая определить приближённое значение корня (с недостатком):
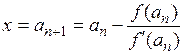 (n = 0, 1, 2, 3, …),
(n = 0, 1, 2, 3, …),
здесь за 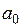 принимается левая граница промежутка изоляции корня (рис.21).
принимается левая граница промежутка изоляции корня (рис.21).
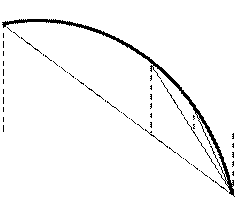
Рассмотрим ещё один метод уточнения корней уравнения – метод секущих(или метод хорд). Согласно этому методу в качестве приближённых значений корня уравнения 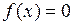 выбираются абсциссы точек пересечения с осью (Оx) секущих, соединяющих граничные точки графика
выбираются абсциссы точек пересечения с осью (Оx) секущих, соединяющих граничные точки графика 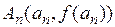 и
и 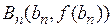 , полученные на n-ом шаге (n = 0, 1, 2, …) . Секущие соответствуют последовательности «вложенных» отрезков
, полученные на n-ом шаге (n = 0, 1, 2, …) . Секущие соответствуют последовательности «вложенных» отрезков
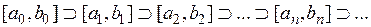 ,
,
где в случае (I): 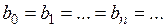 ;
; 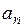 –значения корня с недостатком;
–значения корня с недостатком;
в случае (II):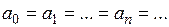 ;
; 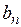 –значения корня с избытком (рис. 22).
–значения корня с избытком (рис. 22).
Составим уравнение секущей (или хорды) 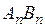 в двух возможных формах:
в двух возможных формах:
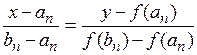 или
или 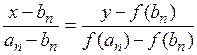 .
.
Вычислим абсциссу 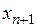 точки пересечения
точки пересечения 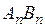 с осью (Оx), положив для этого в указанных уравнениях
с осью (Оx), положив для этого в указанных уравнениях 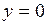 :
:
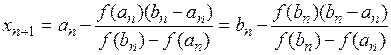 ,
,
здесь в случае (I): 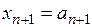 – значение корня с недостатком,
– значение корня с недостатком,
в случае (II): 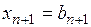 –значение корня с избытком (n = 0, 1, 2, 3, …).
–значение корня с избытком (n = 0, 1, 2, 3, …).
Таким образом, получили две рекуррентные формулы метода хорд.
 y
y
y=f(x)
 | |||||
 | |||||
 | |||||
 0 a0=x0 x1=b1 x2=b2 b0 x
0 a0=x0 x1=b1 x2=b2 b0 x
Рис. 22
|
|
|
© helpiks.su При использовании или копировании материалов прямая ссылка на сайт обязательна.
|