Глава 4. ПРИБЛИЖЁННОЕ РЕШЕНИЕ УРАВНЕНИЙ

Стр 1 из 3Следующая ⇒

Глава 4. ПРИБЛИЖЁННОЕ РЕШЕНИЕ УРАВНЕНИЙ

4.1. Постановка задачи приближённого решения уравнений

Методы приближенного нахождения корней уравнения и оценки их точности применяются, если:

- уравнение достаточно сложное, его корни трудно или невозможно найти аналитическими методами;

- уравнение само содержит коэффициенты, известные только приближенно.

Постановка задачинахождения приближенных корней уравнения

Дано: 1) уравнение вида ;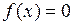

2) функция 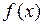непрерывна на некотором отрезке [a, b].

Требуется найти приближённое значение 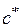корня 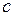данного уравнения, расположенного на отрезке [a, b] ( , ).

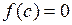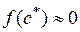Будем считать, что уравнение 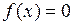имеет изолированные корни, то есть для каждого корня 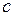существует окрестность 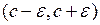, где 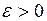, не содержащая других корней уравнения.

Процесс приближенного отыскания корней уравнения содержит два этапа: 1) отделение корней, 2) уточнение корней. Отделить корень 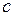– значит, указать такой конкретный промежуток [a, b] (так называемый промежуток изоляции корня), в котором содержится этот и только этот корень. Уточнить корень 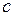с погрешностью 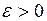– значит, найти такое число 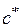, для которого выполняется неравенство 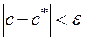, то есть указать промежуток 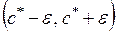, содержащий точный корень уравнения.

В произвольном варианте задача отделения корней сложна, так как эффективных методов ее решения в общем виде не существует. Но для случая достаточно простых функций 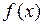наиболее доступным методом отделения корней уравнения является графический метод, состоящий в том, что: 1) либо строится график функции 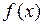, и по нему определяются промежутки, содержащие абсциссы точек пересечения графика с осью (Оx); 2) либо уравнение 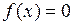заменяется ему равносильным 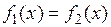, где

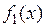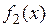, – еще более простые функции, далее строятся графики этих функций и находятся промежутки, содержащие абсциссы их точек пересечения (рис. 19).

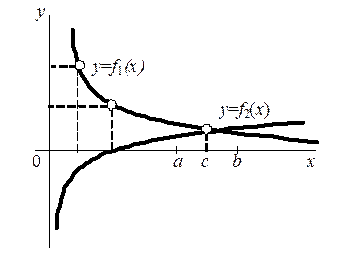
Рис. 19

Ещё один метод отделения корней – табличный – основан на теореме Больцано – Коши об обращении непрерывной функции в нуль. Согласно этому методу вычисляются значения функции 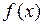в некоторых точках 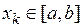: 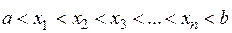, и в случае, если окажется 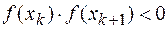, очевидно, существует хотя бы один корень уравнения 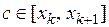; если, кроме того, производная 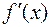сохраняет знак на отрезке 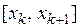, то есть 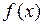монотонна на 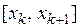, то 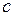- единственный корень уравнения на отрезке .

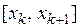Пример.Определить промежуток изоляции корня уравнения .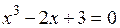

Решение. Если записать данное уравнение по-другому:

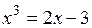построить графики двух получившихся функци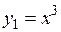й и 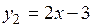, то можно легко увидеть, что абсцисса точки пересечения графиков и есть единственный корень данного уравнения 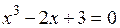, расположенный на отрезке 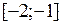, который и является промежутком изоляции корня.

12 3 Следующая ⇒